Траектория движения материальной точки на плоскости XOY представ- ляет собой ломаную линию, выходящую из начала координат вправо и вверх. Вначале точка проходит полуинтервал [0,1) оси абсцисс, а в даль-
нейшем при прохождении точек с абсциссами 1, 2, 3, …, n изменяет направление движения, остающегося прямолинейным, так, что угол между
этим направлением и осью абсцисс увеличивается на
в каждой такой
точке. Найти путь, который пройдет точка, пока ее абсцисса не достиг-
нет величины n
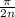
Другие вопросы по теме Геометрия
Популярные вопросы
- Для швейной мастерской купили три ножницы или трое ножниц?...
3 - План описания восточной европейской равнины по плану...
3 - 326 русс.яз 8 класс л. а. мурина 2018 со всеми объяснениями знаков препинания,...
1 - На рисунке 157 изображены ab и ac и ось l шестиугольника...
2 - Решить уравнение. если можно то подробно....
3 - Терміново потрібно)) будь ласочка іть) буду вдячна! 30 ів...
3 - Пятый класс коровина страница 154 - 155 написать основную мысль текста...
1 - Надо разделить на несколько столбиков что делал что наблюдал уравнения...
3 - На тело массой 4 кг действует сила 10н , в результате чего скорость...
3 - 29 . люди,мне нужно сочинение про здоровый образ жизни только простыми...
3
Начальный отрезок траектории проходит по полуинтервалу [0,1) оси абсцисс. Затем, когда точка достигает абсциссы 1, 2, 3, ..., n, направление ее движения меняется так, чтобы угол между этим направлением и осью абсцисс увеличивался на π/2n в каждой такой точке.
Нам нужно найти путь, который точка пройдет, пока ее абсцисса не достигнет значения n.
Пошаговое решение:
1. Найдем угол между движением точки и осью абсцисс в начале ее движения (при абсциссе 0). Так как точка движется прямолинейно вправо, этот угол равен 0.
2. Для каждой абсциссы от 1 до n посчитаем изменение угла движения на π/2n. При абсциссе 1 угол равен π/2n, при абсциссе 2 угол равен 2π/2n, и так далее.
3. Сложим все углы, чтобы получить общее изменение угла движения точки.
4. Общий путь, который пройдет точка, можно найти, используя формулу длины дуги окружности: длина_дуги = радиус * угол_в_радианах. Так как точка движется по прямым участкам и каждый раз меняет направление при достижении абсциссы, мы можем разбить ее траекторию на части и посчитать длину каждой части отдельно.
Это пошаговое решение задачи, которое позволяет школьнику понять основные шаги и обоснования, применяемые для нахождения пути, пройденного точкой до достижения абсциссы n.