Точки m, n и p лежат на сторонах ав, вс, ас треугольника авс, причем am/ab= bn /bc= cp /ca = 1/ 3 . прямые см, an, bp, пересекаясь, ограничивают треугольник, площадь которого равна s. найдите площадь треугольника abc

Ответы

udekhdhdj 08.07.2020 13:21

Положим что треугольник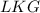 LKG площадь котрого равна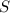

По теореме Менелая , получим соотношения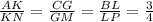 $\frac{AK}{KN} = \frac{CG}{GM}=\frac{BL}{LP} = \frac{3}{4}$

$\frac{BG}{GP}=\frac{AL}{LN}=\frac{CK}{KM}=6$

Допустим угол между сторонами меньшего треугольника равны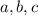 a,b,c

$KL=\frac{3AN}{7}$

$LG=\frac{3BP}{7}$

$LG=\frac{3CM}{7}$

$\frac{\frac{9AN*BP}{49}*sina}{2}=S$

$\frac{\frac{3*BP*6AN}{49}*sina}{2}=2S$

То есть площадь треугольника

$S_{ABC}=7S$

ПОКАЗАТЬ ОТВЕТЫ

andron92 08.07.2020 13:21

Проведем HS || AB. Обозначим SH=m SP=c
треугольники AMC и SHC подобны как и треугольники ABP и SHP.
Дальше просто поиграем с отношениями:
x/m=3z/(z+c)
3x/m=2z/c
поделим одно на второе:
3=2/c * (z+c)/3=2(z+c)/3c
9c=2z+2c
2z=7c
c=2z/7
MC/HC=3z/(z+c)=3z/(z+2z/7)=3/(9/7))=7/3
Ну еще для достижения успеха нужно найти отношения:
BH/Hf и MH/Hg. В целом это та же игра отношений. Хотя иногда эта игра бывает такой сложной,что средний ум бы с ней не справился, что делает сам процесс игры с отношениями весьма увлекательным занятием :)
Пусть Bp=j Bp/Hp=2z/c=2z/(2z/7)=7
Hp=j/7.
В силу симметрии задачи(на каждой стороне те же отношения )
Bp/Bf=7/3
Bf=3j/7
Откуда: fH=j-j/7-3j/7=3j/7
HB=j-j/7=6j/7
BH/fH=6/7*7/3=2 :)
Осталось еще 1 отношение
MH/Hg но в целом из симметрии выходит что по тем же принципам: MC=k Mg=k/7 Hg=3k/7 :)
MH/Hg=4/7 *7/3=4/3
Ну вот и вся задача осталось поиграть с площадями. :)
SBMH=4/3*2*S=8/3 S
SBMC=8/3*7/4S=14S/3
SABC=14S/3*3/2=7S
Сошлось :) Я саму игру площадей не расписывал если нужно напишу.

.

Точки m, n и p лежат на сторонах ав, вс, ас треугольника авс, причем am/ab= bn /bc= cp /ca = 1/ 3 .