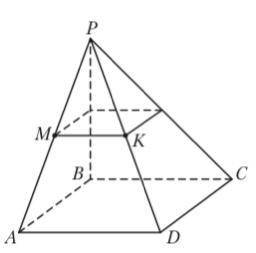
Точки M и K — середины ребер PA и PD четырехугольной пирамиды PABCD. Периметр основания пира- миды равен 16 см. Периметр сечения пирамиды плоскостью, проходящей через точки M и K параллельно пря- мой AB, равен: а) 4 см; в) 12 см; б) 8 см; г) 16 см

Для решения этой задачи мы воспользуемся свойствами серединных перпендикуляров в треугольниках и свойствами параллельных прямых.

Дано, что точки M и K - середины ребер PA и PD. Значит, отрезки PM и PK являются серединными перпендикулярами к сторонам AB и CD соответственно.

Так как PM является серединным перпендикуляром к стороне AB, то он делит эту сторону пополам. Аналогично, PK делит сторону CD пополам.

Теперь посмотрим на сечение пирамиды плоскостью, проходящей через точки M и K параллельно прямой AB. Это сечение будет параллелограммом, так как серединные перпендикуляры в треугольниках создают параллелограмм в сечении.

Таким образом, мы можем выделить два треугольника: один на основании пирамиды ABCD и второй на сечении, образованном точками M и K.

Поскольку периметр основания пирамиды равен 16 см, а AB - одна из сторон основания, то AB = 16/4 = 4 см.

Так как PM делит сторону AB пополам, то AM = AB/2 = 4/2 = 2 см.

Аналогично, так как PK делит сторону CD пополам, то DK = CD/2 = AB/2 = 4/2 = 2 см.

Теперь посмотрим на сечение. Учитывая, что M и K являются серединами сторон основания пирамиды, а сечение проходит параллельно AB, мы можем сказать, что сторона параллелограмма, соответствующая AB, также должна быть равна AB.

Таким образом, периметр сечения пирамиды равен 2 * (AB + CD) = 2 * (4 + 4) = 2 * 8 = 16 см.

Ответ: г) 16 см.