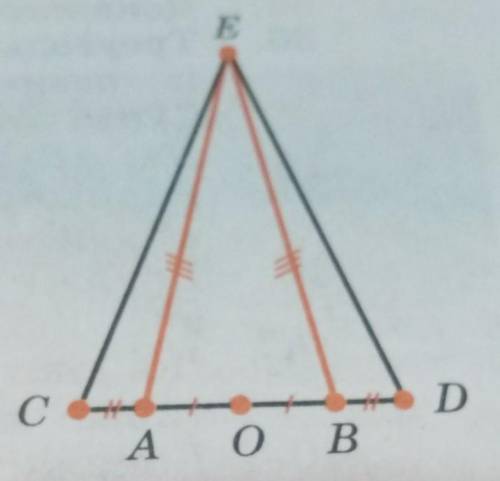
точки A, B, C, D лежат на одной прямой, причём отрезки AB И CD имеют общую середину. Докажите, что если треугольник ABE равнобедренный с основанием AB, то треугольник CDE тоже равнобедренный с основанием CD (рисунок)

Для начала разберемся с геометрической моделью, описанной в вопросе. У нас есть четыре точки A, B, C и D на одной прямой. Отрезки AB и CD имеют общую середину E. Нам нужно доказать, что треугольник ABE равнобедренный с основанием AB, то треугольник CDE тоже равнобедренный с основанием CD.

Для доказательства этого утверждения мы можем использовать расстояние между точками на прямой.

Шаг 1: Докажем, что отрезки AE и DE имеют одинаковую длину.

Из условия задачи мы знаем, что точка E является серединой отрезков AB и CD. Поэтому, мы можем сказать, что длина AE равна длине BE, и длина DE равна длине CE.

Шаг 2: Рассмотрим треугольники ABE и CDE.

У нас есть равные длины отрезков AE и DE. Теперь посмотрим на углы ABЕ и CDЕ.

Шаг 3: Докажем, что углы ABЕ и CDЕ равны.

Мы знаем, что треугольник ABE равнобедренный с основанием AB, что означает, что углы ABЕ и BAE равны. Также, у нас есть AB // CD, поэтому угол BAE равен углу CED (это также можно доказать, используя свойства параллельных прямых и траснверсальных углов).

Итак, у нас есть две пары равных углов: ABЕ и CDЕ, и BAE и CED.

Шаг 4: Докажем, что треугольник CDE равнобедренный с основанием CD.

Нам нужно доказать, что длина CE равна длине DE (то есть треугольник CDE равнобедренный) с основанием CD.

Мы уже доказали, что углы ABE и CDЕ равны, и длина AE равна длине DE. Теперь рассмотрим треугольник CDE: у нас есть равные углы CED и BAE, и равные длины DE и AE.

Значит, треугольник CDE равнобедренный с основанием CD.

Таким образом, мы доказали, что если треугольник ABE равнобедренный с основанием AB, то треугольник CDE тоже равнобедренный с основанием CD.

Это решение основано на свойствах параллельных прямых и равенсте величин. Можно также рассмотреть другие подходы к доказательству этого утверждения, но данный способ является наиболее простым и понятным для школьного уровня.