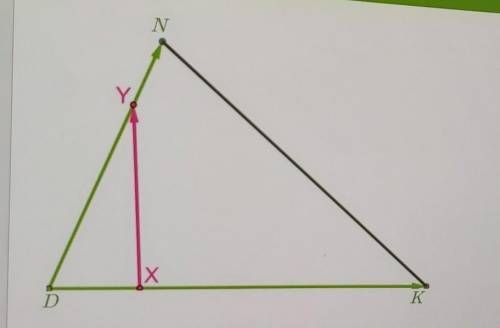
Точка x делит сторону KD в отношении KX:XD= 2:1 , точка Y делит сторону DN в отношении DY:YN= 2:1 Разложи вектор XY по векторам DK и DN
XY= ​

Для того чтобы разложить вектор XY по векторам DK и DN, нам необходимо найти длины векторов DK и DN, а затем найти их пропорцию.

Из условия задачи мы знаем, что точка X делит сторону KD в отношении KX:XD=2:1. Это значит, что отрезок KX составляет две части отрезка XD, а отрезок XD составляет одну часть отрезка KD. Обозначим длину отрезка KD как d. Тогда длина отрезка KX равна 2d/3, а длина отрезка XD равна d/3.

Аналогично, точка Y делит сторону DN в отношении DY:YN=2:1. Это значит, что отрезок DY составляет две части отрезка YN, а отрезок YN составляет одну часть отрезка DN. Обозначим длину отрезка DN как e. Тогда длина отрезка DY равна 2e/3, а длина отрезка YN равна e/3.

Теперь мы можем найти длину вектора XY. Вектор XY - это разность координат точек X и Y. Пусть координаты точки X равны (x1, x2), а координаты точки Y равны (y1, y2). Тогда вектор XY можно выразить следующим образом:

XY = (y1 - x1, y2 - x2)

Теперь разложим вектор XY по векторам DK и DN. Для этого нужно найти коэффициенты, с которыми вектора DK и DN входят в состав вектора XY.

Для разложения вектора XY по вектору DK, нужно найти коэффициент tk. Вектор DK можно выразить как D - K. Это означает, что вектор DK = (d, 0), так как точка D находится на оси X в начале координат, а точка K находится d единиц от нее.

Итак, вектор DK = (d, 0). Чтобы выразить вектор XY через вектор DK, нужно найти коэффициент tk. Для этого нужно разделить скалярное произведение векторов XY и DK на квадрат длины вектора DK:

tk = (XY * DK) / (DK * DK),

где * обозначает скалярное произведение векторов.

Скалярное произведение векторов XY и DK равно x1*d. Скалярное произведение DK и DK равно d*d. Таким образом, мы получаем:

tk = (x1*d) / (d*d) = x1 / d.

Теперь мы знаем коэффициент tk. Чтобы найти разложение вектора XY по вектору DK, нужно умножить вектор DK на этот коэффициент:

( x1 / d ) * ( d, 0 ) = ( x1, 0 ).

Таким образом, разложение вектора XY по вектору DK будет равно (x1, 0).

Аналогично, для разложения вектора XY по вектору DN нужно найти коэффициент tn. Вектор DN можно выразить как D - N, так как точка D находится на оси X в начале координат, а точка N находится на оси Y:

DN = (d, -e).

Теперь, чтобы выразить вектор XY через вектор DN, нужно найти коэффициент tn. Для этого нужно разделить скалярное произведение векторов XY и DN на квадрат длины вектора DN:

tn = (XY * DN) / (DN * DN),

где * обозначает скалярное произведение векторов.

Скалярное произведение векторов XY и DN равно x1*(-e). Скалярное произведение DN и DN равно d*(-d) + e*(-e) = d^2 + e^2. Таким образом, мы получаем:

tn = (x1 * (-e)) / (d^2 + e^2).

Теперь мы знаем коэффициент tn. Чтобы найти разложение вектора XY по вектору DN, нужно умножить вектор DN на этот коэффициент:

tn * (d, -e) = ( -tn * e, tn * d ).

Таким образом, разложение вектора XY по вектору DN будет равно ( -e * (x1 * (-e)) / (d^2 + e^2), d * (x1 * (-e)) / (d^2 + e^2) ).

Таким образом, ответ на задачу будет следующим:

XY = (x1, x2),
DK = (x1, 0),
DN = ( -e * (x1 * (-e)) / (d^2 + e^2), d * (x1 * (-e)) / (d^2 + e^2) ).

Пожалуйста, обратите внимание, что это только математическое решение задачи, и в реальной жизни мы использовали бы компьютер или программу для выполнения всех этих вычислений.