Точка Р принадлежит стороне АD квадрата ABCD, а точка О приналежит диагонали АС, причем АP:АD=1:3 и ОС=
см.Вычислите площадь четырехугольника POCD, если известно, что около него можно описать окружность.
Другие вопросы по теме Геометрия
Популярные вопросы
- ❤❤❤для мегамозгов❤1)плотность тока при серебрении контактов провода равна 40 а/м²....
3 - Вставь пропущенный знак! -3 + ? = 6...
2 - Массу солнца, считая, что скорость вращения земли вокруг солнца 30 км / с, а радиус...
3 - 15 . найдите значение выражения наиболее удобным если x=3,54: (x+7)^2-2(x+7)(x-5)^2+(x-5)^2...
3 - Разложить на множители: 1)20ху-5х²-20у²; 2)12ab-2a²-18b²....
3 - 2целое число разделить 6/7разделить 14/15...
2 - Массовая доля кислорода в серной к-те 1. 65,3 % 2. 50% 3. 35,5% 5.32,6%...
2 - 18 умоляю 1. вид кіно, у якому сюжет втілюється за знятих на плівку малюнків, об’ємних...
3 - Из точки b, не лежащей на плоскости альфа, проведена наклонная вс=12 см, составляющая...
1 - Вынеси общий множитель за скобки a9b2−ab7...
2
Пусть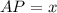 и
и  . Около четырехугольника вписали окружность, следовательно,
. Около четырехугольника вписали окружность, следовательно,  . Следовательно, OP ⊥ AC. Отсюда ΔAOP - равнобедренный прямоугольный треугольник.
. Следовательно, OP ⊥ AC. Отсюда ΔAOP - равнобедренный прямоугольный треугольник.
Прямоугольные треугольники AOP и ACD подобны по двум углам
Площадь четырехугольника POCD:
ответ: 272.