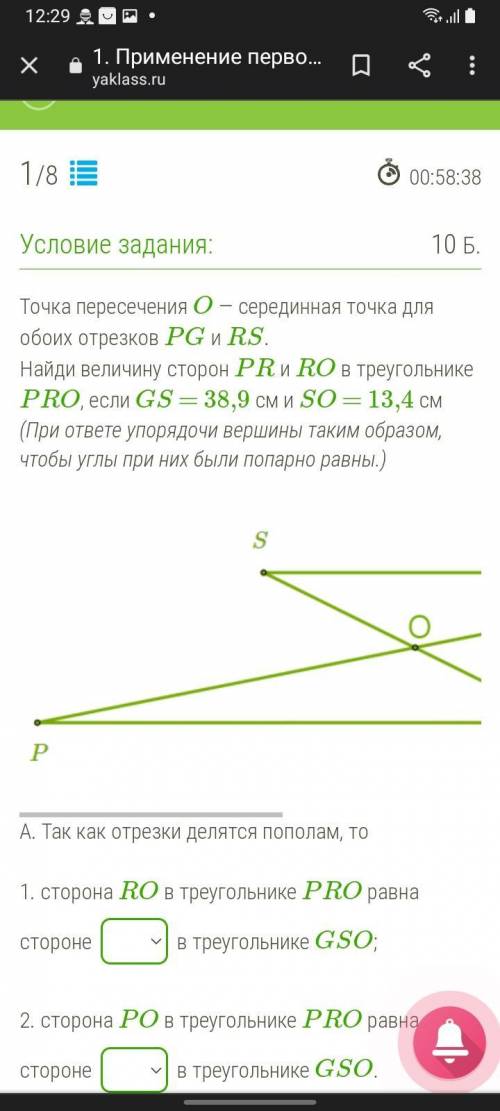
Точка пересечения O — серединная точка для обоих отрезков PG и RS. Найди величину сторон PR и RO в треугольнике PRO, если GS = 38,9 см и SO = 13,4 см (При ответе упорядочи вершины таким образом, чтобы углы при них были попарно равны.) PS1.png А. Так как отрезки делятся пополам, то 1. сторона RO в треугольнике PRO равна стороне в треугольнике GSO; 2. сторона PO в треугольнике PRO равна стороне в треугольнике GSO. Угoл ROP равен углу как вертикальный угол. Треугольники равны по первому признаку равенства треугольников. В равных треугольниках соответствующие стороны равны. PR = см; RO = см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите систему x-y=- 7 xy- 4y+x- 4=0...
1 - Решить цепочку ch3oh-ch3br-c2h6-c2h5cl-c2h5oh...
1 - Чашка, которая стоила 90 рублей, продается с 10%-й скидкой. при покупке 10 таких...
1 - Расстояние 320 км моторная лодка проходит по течению реки за 8 ч, а против течения...
1 - Формула взаимосвязи масс и температур жидкостей при их смешивании...
1 - Портной имеет кусок сукна в 16 метров,от которого он отрезает по 2 метра. на какой...
1 - Які речовини взаємодіють з h2so4: koh, h2o, mg?...
1 - Особенности внешней политики в середине 1950–начале 60-х гг. её противоречивый характер...
1 - Ученик выполнил : «нарисовать ход луча света, из воздуха перпендикулярно поверхности...
1 - Выписано несколько последовательных членов арифметической прогрессии: ; 17; х; 13;...
3
Дано, что точка О - серединная точка для отрезков PG и RS. То есть, отрезки PG и RS равны между собой.
Мы знаем, что GS = 38,9 см и SO = 13,4 см.
Вопрос заключается в том, чтобы найти величину сторон PR и RO в треугольнике PRO.
1. Согласно условию, точка O является серединной точкой для отрезка PG. Поэтому, сторона RO в треугольнике PRO будет равна стороне GS.
RO = GS = 38,9 см.
2. Также, согласно условию, точка O является серединной точкой для отрезка RS. Поэтому, сторона PO в треугольнике PRO будет равна стороне SO.
PO = SO = 13,4 см.
3. Угол ROP равен углу как вертикальный угол. Вертикальные углы равны между собой (согласно свойству вертикальных углов).
∠ROP = ∠GOS.
4. Треугольники PRO и GOS равны по первому признаку равенства треугольников (ППРТ). Поэтому, соответствующие стороны этих треугольников равны.
PR = GS = 38,9 см.
RO = SO = 13,4 см.
Таким образом, величина стороны PR равна 38,9 см, а величина стороны RO равна 13,4 см.
Надеюсь, ответ был достаточно подробным и понятным для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать.