Точка M делит отрезок ED в отношении EM:MD=2:1. Напиши, на какое число умножить векторы, чтобы равенства получились верными
(в окошко для знака числа запиши «+», если число положительное):
1. EM−→−=
⋅ED−→−;
2. DM−→−=
⋅ED−→−;
3. MD−→−=
⋅EM
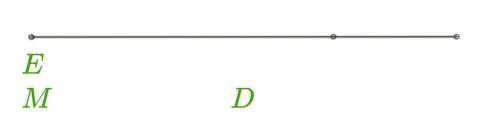
Другие вопросы по теме Геометрия
Популярные вопросы
- нужно провести сечение плоскостей через 3 точки : l, m, k. чертёж и построение....
1 - Дано призму abca1b1c1 і площину,що проходить через прямі ac1 i ab.побудуйте прямі,по...
3 - 7- тапсырма. нарық заманында кәсіпкерге қойылатын талаптарды диаграмма түрінде...
3 - Периметор стола прямоугольной формы 160дм.длина 55дм .узнай площадь стола...
3 - Катер пливе за течією ріки з пункту а в пункт в 3 години а рятівний круг цю відстань...
3 - 10 ! если что там написано: докажите, что значение выражения (пример) является...
2 - Хелп! ! найдите меньшую сторону треугольника со сторонами 9 см. 12 см. 15 см....
3 - Кому не сложно: это. sino+cos(-п/2)+sin^2(п/4).и этот.2cos^2x-sinx+1=0...
2 - Решите, расставьте коэффициенты в уравнениях реакций 1. ph3+o2=p2o5+h2o 2. fe2o3+nho3=fe(no3)3+h2o...
2 - Визнач ціну поділки шкали,верхню і нижню межі вимірювання медичного термометра...
1
1. EM→ ⃗- = ⋅ED→ ⃗
Рассмотрим отношение EM:MD=2:1. Это означает, что отношение величин векторов EM и MD равно 2:1. Так как точка M делит отрезок ED в таком отношении, то вектор ED→ ⃗ будет равен сумме векторов EM→ ⃗ и MD→ ⃗:
ED→ ⃗ = EM→ ⃗ + MD→ ⃗
Мы хотим найти число, на которое нужно умножить векторы, чтобы равенство EM→ ⃗ = ⋅ED→ ⃗ было верным. Так как вектор MD→ ⃗ равен 1/3 вектора ED→ ⃗ (так как EM:MD=2:1), то можно записать:
EM→ ⃗ = ⋅(EM→ ⃗ + MD→ ⃗)
EM→ ⃗ = ⋅((1/3)*ED→ ⃗ + MD→ ⃗)
EM→ ⃗ = ⋅(1/3*ED→ ⃗ + 1/3*ED→ ⃗)
EM→ ⃗ = ⋅(2/3*ED→ ⃗)
Из этого следует, что число, на которое нужно умножить вектор ED→ ⃗, чтобы равенство EM→ ⃗ = ⋅ED→ ⃗ было верным, равно 2/3.
Ответ: ⋅(2/3).
2. DM→ ⃗ = ⋅ED→ ⃗
Аналогично, мы можем рассмотреть отношение MD:EM=1:2 (так как EM:MD=2:1). Тогда вектор MD→ ⃗ будет равен 1/3 вектора ED→ ⃗ и вектор EM→ ⃗ будет равен 2/3 вектора ED→ ⃗. Таким образом, мы можем записать:
DM→ ⃗ = ⋅(1/3* ED→ ⃗)
DM→ ⃗ = ⋅(1/3* (3*MD→ ⃗ + 3*EM→ ⃗))
DM→ ⃗ = ⋅(1/3* (3*MD→ ⃗ + 3*(2/3* ED→ ⃗)))
DM→ ⃗ = ⋅(1/3* (3*MD→ ⃗ + 2* ED→ ⃗))
Из этого следует, что число, на которое нужно умножить вектор ED→ ⃗, чтобы равенство DM→ ⃗ = ⋅ED→ ⃗ было верным, равно 1/3.
Ответ: ⋅(1/3).
3. MD→ ⃗ = ⋅EM→ ⃗
Мы можем использовать то же отношение MD:EM=1:2. Так как вектор EM→ ⃗ равен 2/3 вектора ED→ ⃗, то вектор MD→ ⃗ будет равен 1/3 вектору EM→ ⃗. Таким образом, мы можем записать:
MD→ ⃗ = ⋅(1/3* EM→ ⃗)
MD→ ⃗ = ⋅(1/3* (2*ED→ ⃗))
MD→ ⃗ = ⋅(2/3* ED→ ⃗)
Из этого следует, что число, на которое нужно умножить вектор EM→ ⃗, чтобы равенство MD→ ⃗ = ⋅EM→ ⃗ было верным, равно 2/3.
Ответ: ⋅(2/3).
Таким образом, для всех трех равенств число, на которое нужно умножить векторы, чтобы равенства были верными, равно 2/3.