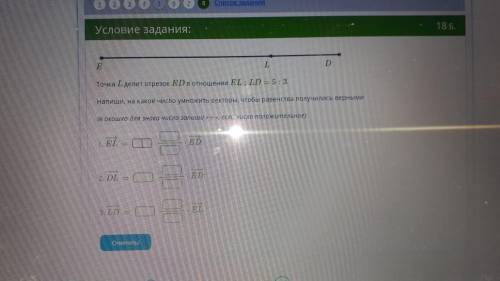
точка L делит отрезок ed,в отношении EL:LD=5:3. напиши на какое число умножить векторы чтобы равенство получилось верным
Другие вопросы по теме Геометрия
Популярные вопросы
- Буква обозначает два звука в словах: юбка,вишня,мяч...
2 - Найти сторону треугольника, если противолежащий ей угол равен 60градусов,...
3 - Определите, какое из указанных имен файлов удовлетворяет маске: ? hel*lo.c?...
1 - Предложения со словами краски колос инкубатор огурцы на завтра...
2 - Как вы озаглавите текст: потекли ручьи. под крышами ласточки вьют гнезда....
1 - 1. найти те элементы массива, которые равны сумме двух своих соседей. первый...
1 - Решить 9т 7кг - 13ц 36 кг 6ч 28 мин + 19 ч 43 мин 12м 5дм - 6м 7см !...
3 - Выразите в квадратных миллиметрах : 6 квадратных см. 15мм квадратных,3дм...
2 - Найдите общий вид первообразных для функции f(x)=2x^2+6...
2 - Что такое хлеб промышленость (промышлености) и что такое горный лён...
1
Вектор EL можно представить как сумму двух векторов: EA и AL, тогда можно записать векторное равенство EL = EA + AL.
Вектор LD можно представить как разность двух векторов: LE и ED, тогда можно записать векторное равенство LD = LE - ED.
По условию, отношение EL:LD равно 5:3. Векторно это можно записать так: EL/LD = 5/3.
Тогда мы можем записать следующее уравнение:
(EL/LD) = (EA + AL)/(LE - ED) = 5/3
Чтобы избавиться от дробей, умножим нижнюю и верхнюю часть уравнения на 3:
3(EA + AL) = 5(LE - ED)
Раскрываем скобки:
3EA + 3AL = 5LE - 5ED
Теперь у нас есть уравнение, в котором участвуют только векторы EA, AL, LE и ED. Нам нужно найти число, на которое нужно умножить векторы EA, AL, LE и ED, чтобы равенство выполнилось.
Очевидным решением является умножение на число 3, чтобы уравнение выполнилось:
3(EA + AL) = 5(LE - ED)
Можем проверить это:
3(EA + AL) = 5(LE - ED)
3E + 3A + 3L = 5L - 5E + 5D
3E + 3A + 3L = 5L - 5E + 5D
Оба равенства выполняются, значит, число 3 является ответом на задачу: нужно умножить все векторы на 3, чтобы равенство было верным.