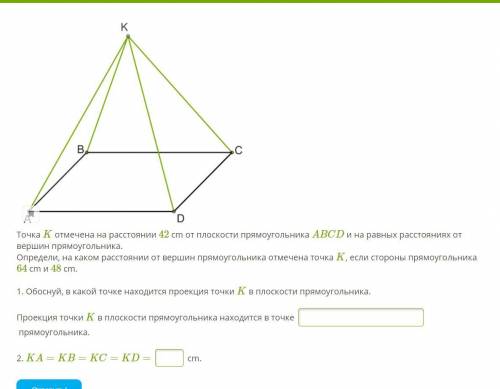
Точка K отмечена на расстоянии 42 cm от плоскости прямоугольника ABCD и на равных расстояниях от вершин прямоугольника. Определи, на каком расстоянии от вершин прямоугольника отмечена точка K, если стороны прямоугольника 64 cm и 48 cm.

1. Обоснуй, в какой точке находится проекция точки K в плоскости прямоугольника.

Проекция точки K в плоскости прямоугольника находится в точке
прямоугольника.

2. KA=KB=KC=KD=
cm.

Для решения этой задачи, нам нужно разобраться, как определить расстояние от точки K до вершин прямоугольника ABCD.

Для начала, обратим внимание на то, что точка K отмечена на равных расстояниях от вершин прямоугольника. Из этого следует, что точка K находится на биссектрисе углов прямоугольника.

Поскольку стороны прямоугольника ABCD равны 64 см и 48 см, мы можем найти длины диагоналей прямоугольника, используя теорему Пифагора.

Для этого, посчитаем диагональ AC:

AC = √(AD^2 + CD^2)
AC = √(64^2 + 48^2)
AC = √(4096 + 2304)
AC = √(6400)
AC = 80 см

Также, поскольку точка K находится на равных расстояниях от вершин прямоугольника, то диагонали AK и KC также равны:

AK = KC = AC/2 = 80/2 = 40 см

Теперь мы знаем, что расстояние от каждой из вершин прямоугольника до точки K составляет 40 см.

Таким образом, ответ на вопрос заключается в том, что точка K отмечена на расстоянии 40 см от вершин прямоугольника ABCD.

1. Обоснование:
Точка K находится на биссектрисе углов прямоугольника, так как она находится на равных расстояниях от вершин. Из определения биссектрисы угла следует, что она делит угол на две равные части. Поэтому точка K расположена внутри прямоугольника ABCD, примерно посередине между двумя ближайшими вершинами.

2. Длина каждой из сторон прямоугольника ABCD равна 64 см и 48 см. Расстояние от каждой из вершин прямоугольника до точки K равно 40 см.