 диаметр окружности с центром в точке
диаметр окружности с центром в точке  ,
,  хорда окружности,
хорда окружности,  ⊥
⊥ ,
,  ∈
∈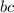 . найдите удвоенную площадь треугольника
. найдите удвоенную площадь треугольника 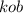 .
.
Другие вопросы по теме Геометрия
Популярные вопросы
- Есть ли ошибки или неверные суждения в предложении? А) Неологизмы в основном...
3 - Риторический вопрос ставится для того, чтобы привлечь внимание художественное...
3 - Конкретно-исторические темы - характеры и обстоятельства, носящие вневременной,...
3 - Верны ли утверждения? А) Литературно-условные и непосредственно-достоверные...
2 - Архаизмы - те слова, которые вышли из общего употребления, потому что утратились...
3 - Эстетическое воздействие художественного произведения на читателя обусловлено...
3 - Верны ли утверждения? А) Количественная метонимия получила название метафоры...
3 - По жанровой принадлежности «Сон в летнюю ночь» У. Шекспира - комедия роман...
3 - Общекультурный феномен, окончательно сформировавшийся в 70-80-ые гг. ХХ века...
1 - Верны ли утверждения? А) В высказывании «железная воля» есть метафора...
3
Вписанный угол ACB опирается на диаметр AB, следовательно, ∠ACB = 90°, тогда по теореме Пифагора:
Далее у треугольников ABC и KOB ∠B общий и углы прямые равны, значит эти треугольники подобны по двум углам. Коэффициент подобия: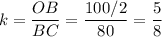
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отсюда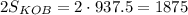 кв. ед.
кв. ед.
ответ: 1875 кв. ед.