Тема: теорема о трёх перпендикулярах , с последней задачей.
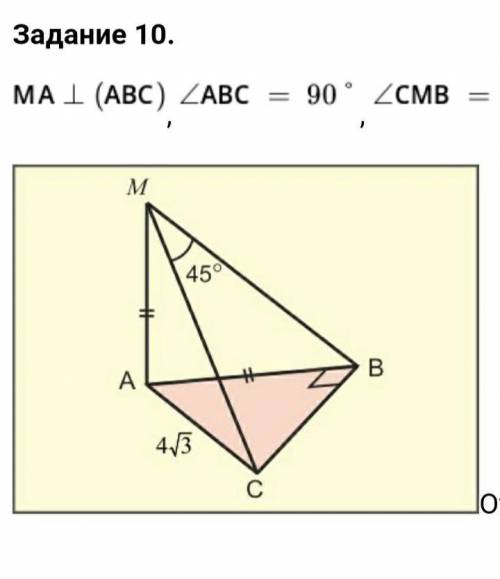
Начало условия на фото.
Уг. СМВ = 45°, МА = АВ, АС = 4√3
Найти МС.
, с объяснением.
Другие вопросы по теме Геометрия
Популярные вопросы
- Доказать с кругов Эйлера - Венна справедливость следующего равенства...
3 - UK: May DayMay Day is a spring 1) (CELEBRATE)that takes place on the...
2 - Решите В правильном тетраэдре ребро равно 6 см. найдите высоту и полную...
3 - Підсумкова контрольно - діагностична робота Варіант 1 І – ІІ рівень ,...
3 - Установiть вiдповiднiсть мiж речовиною та ii використанням 1.Глюкоза...
1 - Написать эссе рассуждение.На тему что бы я изменил в мире имея не больше...
2 - 00 гоИ.А. Крыл.ким юморомется ирония (т.л Крылов острекозе говорит с...
1 - До якого міста приїхали заморські гості з однойменної гуморески?...
3 - Dear Mum and Dad. I m having a greattime here! We play football day andnight....
3 - Какого расщепления в потомстве по генотипу и фенотипу можно ожидать,...
3
Пусть МА будет х, тогда АВ тоже будет х.
∆МАВ- прямоугольный равнобедренный треугольник.
МВ=√(МА²+АВ²)=√(х²+х²)=х√2
АВ⊥ВС, по условию
МВ⊥ВС, по Теореме о трех перпендикулярах.
∆МСВ- прямоугольный равнобедренный треугольник. Углы при основании равны. ∠СМВ=∠МСВ=45°
МВ=СВ=х√2.
∆АВС- прямоугольный треугольник
По Теореме Пифагора
АС²=АВ²+ВС²
Уравнение:
х²+(х√2)²=(4√3)²
х²+2х²=48
3х²=48
х²=48/3
х=√16
х=4 ед МА
∆МАС- прямоугольный треугольник
По теореме Пифагора
МС=√(МА²+АС²)=√(4²+(4√3)²)=
=√(16+48)=√64=8 ед.
ответ: МС=8ед.