Тема сумма углов треугольника решить пару задачку, я никак их не пойму)

Объяснение:

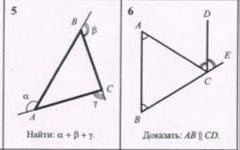
5. Есть в принципе теорема, что сумма внешних углов равно 360°. Но можно для этой задачи расписать:

α=<B+<C; β=<A+<C; γ=<A+<B - по теореме "Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом."

Получается α+β+γ=<B+<C+<A+<C+<A+<B=2*(<A+<B+<C)=2*180=360°

6. <ACE - внешний для угла <ACB => <ACE=<ABC+<BAC, и углы <ABC и <BAC равны по условию.

При этом <ACE=<ACD+<ECD и <ACD и <ECD также равны между собой по условию. Значит <BAC=<ACD - а это накрест лежащие углы при прямых AB и CD и секущей АС. => AB || CD чтд.