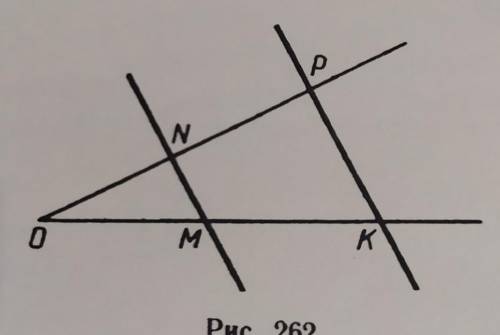
ТЕМА: ПОДОБИЕ ТРЕУГОЛЬНИКОВ. На рисунке ОМ = 13,5 см, ОК— 27 см, ON = 5,5 см, OP= 11см. а) Докажите, что прямые MN и КР параллельны. б) Найдите отношение площадей и периметров треугольников OMN и ОКР.

Добрый день! Давайте рассмотрим ваш вопрос о подобии треугольников и докажем, что прямые MN и КР являются параллельными.

Для начала, давайте обратимся к теории подобия треугольников. По определению, два треугольника считаются подобными, если их соответствующие углы равны, а их соответствующие стороны пропорциональны.

Теперь, чтобы доказать, что прямые MN и КР являются параллельными, мы можем использовать теорему о параллельных прямых и подобных треугольниках. Согласно данной теореме, если в двух треугольниках соответствующие стороны пропорциональны, то прямые, которые соединяют соответствующие вершины треугольников, будут параллельными.

У нас есть треугольники OMN и OKP с соответствующими сторонами OM и OK, ON и OP. Для доказательства, что прямые MN и КР параллельны, нам нужно установить, что соответствующие стороны этих треугольников пропорциональны.

Посмотрим на стороны OM и OK. Из условия задачи мы знаем, что OM = 13,5 см, а OK = 27 см. Разделив OK на 2, мы получим половину его значения, то есть OK/2 = 27/2 = 13,5 см, что равно значению стороны OM. Таким образом, стороны OM и OK равны.

Теперь рассмотрим стороны ON и OP. Из условия задачи мы знаем, что ON = 5,5 см, а OP = 11 см. Если мы разделим ON на 5,5, мы получим значение 1, а если разделим OP на 11, мы также получим значение 1. Значит, стороны ON и OP пропорциональны.

Таким образом, мы доказали, что соответствующие стороны треугольников OMN и OKP пропорциональны. Следовательно, по теореме о параллельных прямых и подобных треугольниках, прямые MN и КР будут параллельными.

Переходим ко второй части вашего вопроса. Нам нужно найти отношение площадей и периметров треугольников OMN и OKP.

Чтобы найти отношение площадей, нам нужно знать соотношение сторон в подобных треугольниках. Но поскольку мы уже доказали, что треугольники OMN и OKP являются подобными, у нас есть пропорциональные стороны OM/OK = ON/OP. Давайте выразим площади треугольников через эти стороны.

Площадь треугольника можно найти, используя формулу: площадь = (основание × высоту) / 2. В треугольнике OMN, основание - это сторона OM, а высота - расстояние, проведенное от вершины N до прямой OM. Пусть это расстояние будет h. Тогда площадь треугольника OMN = (OM × h) / 2.

Аналогично, в треугольнике OKP, основание - это сторона OK, а высота - расстояние, проведенное от вершины P до прямой OK. Пусть это расстояние также будет h. Тогда площадь треугольника OKP = (OK × h) / 2.

Теперь мы можем записать формулы для площадей треугольников:
Площадь треугольника OMN = (OM × h) / 2
Площадь треугольника OKP = (OK × h) / 2

Используя информацию о пропорциональности сторон OM/OK = ON/OP, мы можем записать ON/OP = OM/OK, что можно переписать как ON × OK = OM × OP.

Теперь, если мы заменим OM × OP на ON × OK в формуле для площади треугольника OKP, мы получим:
Площадь треугольника OKP = (ON × OK × h) / 2

Таким образом, отношение площадей треугольников OMN и OKP будет равно:
Площадь OMN / Площадь OKP = ((OM × h) / 2) / ((ON × OK × h) / 2)
= (OM × h) / (ON × OK × h)
= OM / (ON × OK).

Аналогично, мы можем найти отношение периметров этих треугольников. Периметр треугольника - это сумма его сторон. Поэтому отношение периметров будет просто отношением сумм длин сторон:
Периметр OMN / Периметр OKP = (OM + ON + MN) / (OK + OP + KP).

Таким образом, мы получаем, что отношение площадей OMN и OKP равно OM / (ON × OK), а отношение периметров OMN и OKP равно (OM + ON + MN) / (OK + OP + KP).

Вот вам подробное и обстоятельное решение данной задачи. Если у вас остались вопросы или нужно что-то уточнить, я готов вам помочь.