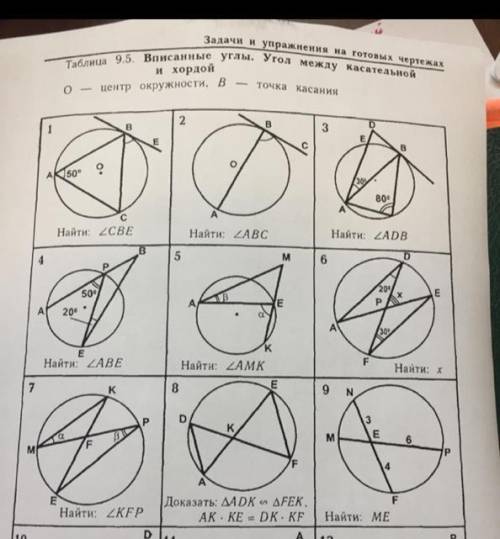
Таблица 9.5. Вписанные углы. Углы между касательной и хордой очень нужно решение и объяснения

На рисунке представлена таблица, которая показывает вписанные углы в окружности. Мы сосредоточимся на углах, образованных касательной и хордой.

1. Угол между касательной и хордой, проходящей через точку касания:
- Этот угол равен половине угла, стоящего на центральной окружности и отвечающего той же дуге, что и пересекаемая им часть хорды.
- Обозначим его как А.

2. Угол между касательной и хордой, не проходящей через точку касания:
- Этот угол равен полусумме углов, стоящих на окружности и отвечающих той же дуге, что и пересекаемая им часть хорды.
- Обозначим его как В.

Теперь рассмотрим конкретные случаи, чтобы объяснить, как использовать эту таблицу для решения задач.

Пример 1:
Пусть у нас есть окружность с центром в точке O. AB - касательная, а BC - хорда. Нам нужно найти угол А.

Шаги решения:
1. Обратимся к таблице и найдем строку, соответствующую касательной. В данном случае, это первая строка.
2. В этой строке найдем столбец, соответствующий хорде, проходящей через точку касания. В данном случае, это второй столбец.
3. В пересечении строки и столбца найдем угол А (равный половине центрального угла AC).

Пример 2:
Пусть у нас есть окружность с центром в точке O. AB - касательная, а AC - хорда. Нам нужно найти угол В.

Шаги решения:
1. Обратимся к таблице и найдем строку, соответствующую касательной. В данном случае, это первая строка.
2. В этой строке найдем столбец, соответствующий хорде, не проходящей через точку касания. В данном случае, это третий столбец.
3. В пересечении строки и столбца найдем угол В (равный полусумме углов, стоящих на окружности и отвечающих дуге АС).

Таким образом, используя данную таблицу, мы можем легко находить вписанные углы между касательной и хордой в окружности. Надеюсь, это объяснение помогло вам понять, как это сделать.