1. Геометрия
  2. Стороны треугольника 8 см,

Стороны треугольника 8 см, 10 см, 16 см. найдите длины сторон треугольника, подобного данному, с коэффициентом 1,5

Julia5415613614 Julia5415613614    2   11.09.2019 09:30    12

Ответы
fffff2098 fffff2098  07.10.2020 07:11
ответ:

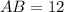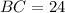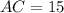AB = 12 см; BC = 24 см; AC = 15 см.

Объяснение:

Обозначим данный треугольник буквами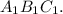 A_1B_1C_1.

A_1B_1 = 8 см.

B_1C_1 = 16 см.

A_1C_1 = 10 см.

Подобный ему треугольник обозначим буквами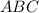 ABC.

Их коэффициент подобия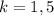 k = 1,5, по условию.

=========================================================

Так как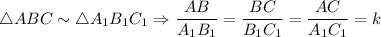 \triangle ABC \sim \triangle A_1B_1C_1 \Rightarrow \dfrac{AB}{A_1B_1} = \dfrac{BC}{B_1C_1} = \dfrac{AC}{A_1C_1} = k

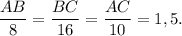
Т.е. \dfrac{AB}{8} = \dfrac{BC}{16} = \dfrac{AC}{10} = 1,5.

Значит:

AB = A_1B_1 \cdot k = 8 \cdot 1,5 = 12\\ см.

BC = B_1C_1 \cdot k = 16 \cdot 1,5 = 24 см.

AC = A_1C_1 \cdot k = 10 \cdot 1,5 = 15 см.


Стороны треугольника 8 см, 10 см, 16 см. найдите длины сторон треугольника, подобного данному, с коэ
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
yurka1973 yurka1973  28.06.2019 14:10
Через вершину b равнобедренного треугольника с основанием ac проведена прямая,параллельная биссектрисе cm этого треугольника и пересекающая прямую,содержащую сторону ac в точке...
Кристалина12 Кристалина12  28.06.2019 14:10
Основа прямого паралепіпеда - паралелограм, стороні якого дорівнюють 3 см і 4 кореня із 2 см, а кут між ними 45 градусів.висота паралепіпеда 6 см. знайти обьєм паралепіпеда....
bbb87 bbb87  28.06.2019 14:10
Втреугольнике abc ас = вс , ah – высота, ab = 5, sin bac =7/25 . найдите bh....
538VICTORIA8425 538VICTORIA8425  28.06.2019 14:10
Постройте равнобедренный треугольник по боковой стороне 5 см,высоте 4 см проведенной к основанию....
Настя20767 Настя20767  07.07.2019 20:40
Основания трапеции относятся как 7: 3 и их разность равна 5,2м.найти среднюю линюю...
TANYA889933 TANYA889933  07.07.2019 20:40
Найдите сторону квадрата, если его площадь равна: 192мм², 2,89см², 18м²...
mranishanbaev mranishanbaev  07.07.2019 20:40
Сторона треугольника равняется 2,4,6, решите треугольник,найти площу, периметр,радиус вписаного и описаного круга,...
Ludmila28041985 Ludmila28041985  15.05.2020 09:15
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = 3. Длины боковых рёбер пирамиды SA = , SB = , SD = а) Докажите, что SA — высота...
Боббоянн Боббоянн  15.05.2020 09:15
В прямоугольный треугольник с катетами 8 и 13 вписана окружность. Найдите ее радиус...
Аринусик111 Аринусик111  15.05.2020 09:17
Диаметр окружности равен 6 см. Около неё описана равнобедренная трапеция, боковая сторона которой 10 см. Вычисли основания и площадь трапеции. Меньшее основание трапеции равно...

Популярные вопросы