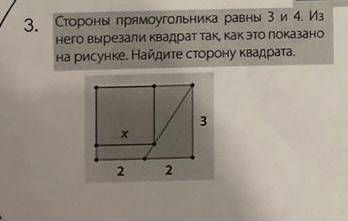
Стороны прямоугольника равны 3 и 4. Из него вырезали квадрат так, как это показано на рисунке. Найдите сторону квадрата.

Добрый день! Для решения данной задачи, сперва необходимо понять, каким образом мы можем найти сторону вырезанного квадрата.

Мы знаем, что стороны прямоугольника равны 3 и 4, и из него вырезали квадрат так, как показано на рисунке. Очевидно, что стороны прямоугольника стали больше после вырезания квадрата, и это поможет нам определить размеры этого квадрата.

После вырезания квадрата, оставшаяся часть прямоугольника больше всего напоминает прямоугольный треугольник. Мы можем воспользоваться нашими знаниями о геометрии треугольников и прямоугольников, чтобы найти сторону вырезанного квадрата.

В данном случае, мы видим, что большая сторона прямоугольника (4) стала основанием прямоугольного треугольника, а меньшая сторона прямоугольника (3) стала одним из катетов этого треугольника. Наша задача - найти другой катет этого треугольника, который и будет являться стороной вырезанного квадрата.

Мы можем использовать один из известных нам теорем Пифагора, которая гласит, что в прямоугольном треугольнике, где квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2.

Запишем данную формулу для нашего треугольника, где a = 3 (меньший катет), b - искомый катет (сторона квадрата) и c = 4 (гипотенуза):

3^2 + b^2 = 4^2

Упростим уравнение:

9 + b^2 = 16

Вычтем 9 из обеих сторон уравнения:

b^2 = 7

Извлечем квадратный корень из обеих сторон уравнения:

b = √7

Вот и ответ! Сторона вырезанного квадрата равна √7 (округляем до двух десятичных знаков).

Мы использовали знания об прямоугольных треугольниках и теореме Пифагора для решения этой задачи. Если у тебя возникнут еще вопросы, не стесняйся задавать!