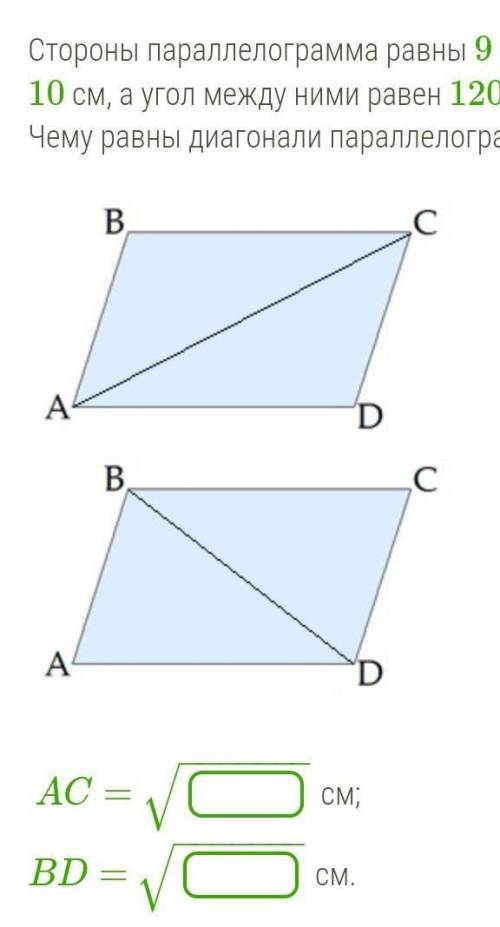
Стороны параллелограмма равны 9 см и 10 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?

Для решения этой задачи нам понадобится знание о свойствах параллелограмма. Одно из этих свойств заключается в том, что диагонали параллелограмма делятся пополам и пересекаются в точке, которая делит их в соотношении 1:1.

В данной задаче мы знаем стороны параллелограмма, которые равны 9 см и 10 см, а также угол между ними, который равен 120°. Нам нужно найти длины диагоналей.

Для начала, давайте рассмотрим треугольник, образованный одной из диагоналей и двумя сторонами параллелограмма. По свойству треугольника сумма углов этого треугольника равна 180°. У нас есть углы 120° и два прямых угла (так как параллелограмм - это четырехугольник с двумя парами параллельных сторон). Таким образом, сумма углов треугольника равна 120° + 90° + 90° = 300°.

Теперь мы можем воспользоваться теоремой косинусов для нахождения длины диагонали параллелограмма.

Вспомним формулу теоремы косинусов: c^2 = a^2 + b^2 - 2ab*cos(C), где c - это длина третьей стороны треугольника, a и b - это длины двух других сторон, а C - это угол между этими сторонами.

Мы хотим найти длину диагонали параллелограмма, поэтому пусть c будет этой длиной. Тогда a будет равна 9 см, b будет равна 10 см, а C будет равен 120°.

Подставим эти значения в формулу теоремы косинусов: c^2 = 9^2 + 10^2 - 2*9*10*cos(120°).

Теперь вычислим значение косинуса 120°. Косинусы углов 60° и 120° имеют значения -0,5 (-0.5). Это можно найти в таблице значений тригонометрических функций или использовать калькулятор. Мы будем использовать значение -0,5.

Подставим это значение в формулу: c^2 = 9^2 + 10^2 - 2*9*10*(-0,5).

Сократим и упростим выражение: c^2 = 81 + 100 + 90.

Сложим числа: c^2 = 181 + 90.

Подсчитаем результат: c^2 = 271.

Чтобы найти длину диагонали параллелограмма, возьмем квадратный корень из обоих сторон: c = √271.

Округлим этот результат до ближайшего целого числа: c ≈ 16,46.

Таким образом, длина диагонали параллелограмма составляет около 16,46 см.

Аналогичным образом мы можем найти и вторую диагональ параллелограмма, поменяв местами значения сторон a и b в формуле теоремы косинусов и получив аналогичный результат.

Надеюсь, это помогло вам разобраться в решении этой задачи, и ответ стал понятен. Если у вас возникнут еще вопросы, пожалуйста, задавайте!