Сторону основания правильной треугольной пирамиды уменьшили в 6 раз, а высоту увеличили в 6 раз. Как изменился объем пирамиды?

Ответы

nikcentennial 11.07.2022 15:41

уменьшится в 6 раз

Объяснение:

s-площадь основания, h-высота, v-объём данной пирамиды

S-площадь основания, H-высота, V-объём изменённой пирамиды

v=sh/3

S=s/6²=s/36

H=6h

V=SH/3=sh/18=v/6

ПОКАЗАТЬ ОТВЕТЫ

dimas194 11.07.2022 15:41

У правильной треугольной пирамиды в основании лежит правильный треугольник ( равносторонний) . Пусть сторона его равна а , высота пирамиды равна Н .

Объём пирамиды равен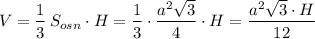 $V=\dfrac{1}{3}\, S_{osn}\cdot H=\dfrac{1}{3}\cdot \dfrac{a^2\sqrt3}{4}\cdot H=\dfrac{a^2\sqrt3\cdot H}{12}$

Если сторону уменьшили в 6 раз, то она стала равна а/6 .

Если высоту увеличили в 6 раз, то она стала равна 6Н .

Объём пирамиды стал равен

$V_1=\dfrac{1}{3}\, S_{osn}\cdot H=\dfrac{1}{3}\cdot \dfrac{(\frac{a}{6})^2\sqrt3}{4}\cdot 6H=\dfrac{1}{3}\cdot \dfrac{a^2\sqrt3}{36\cdot 4}\cdot 6H=\dfrac{a^2\sqrt3\cdot H}{12\cdot 6}=\dfrac{V}{6}$

Объём пирамиды уменьшился в 6 раз .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

romanbeletsky2 24.06.2019 21:30

Если можно с объяснениями )заранее ) величина дуги между двумя окружности = 46 гр. найдите градусную меру вписанного угла, опирающегося на эту дугу....

skZ1 14.12.2020 15:37

Дано точки А(1;-2),В(2;1)С(1;3) Знайти координати вектора АВ. СА...

pervushinapolina 14.12.2020 15:37

Боковая сторона AB равнобедренного треугольника ABC в два раза длиннее основания AC. Рассчитай длины сторон треугольника, если его периметр равен 36 см....

Dameni04 14.12.2020 15:38

Периметр равнобедренного треугольника 3,8 м. боковая сторона больше основания на 1 м.определите длину боковой стороны ...

Vania161 14.12.2020 15:39

Какая игрушка привлекла внимание Мари Щелкунчик и мышиный король...

Nastya4002 14.12.2020 15:40

6 І 2 3 42. Определи координаты букв.DEАС)ВС)СС)543BСDL, )EL, )FC)54321A АF10 1 2 3 4 50 1 2 3 4554определи каргина 2d ...

akjol21 28.04.2020 09:26

1 Verona in Italy is a modern city.2 The Green Bazaar is in Verona.3 Elisha Otis built the first skyscraper.4 Sport centres create unemployment.5 Indians helped build the first skyscraper.6...

алисалисова1611 28.04.2020 09:27

С ГЕОМЕТРИЕЙ 7 КЛАСС ОЧЕНЬ...

Viper397 28.04.2020 09:27

решить во по геометрии 7 класс ...

CISA9999 28.04.2020 09:27

ВСЕ ЗАДАНИЯ И РИСУНКИ В ФОТО Дано: а || b, с - секущая, ∠1 - ∠2 = 102°. Найти: все образовавшиеся углы. Дано: ∠1 = ∠2, ∠3 = 140°. Найти: ∠4. 3. Отрезок АК - биссектриса треугольника...

Сторону основания правильной треугольной пирамиды уменьшили в 6 раз, а высоту увеличили в 6 раз. Как изменился объем пирамиды?

Популярные вопросы