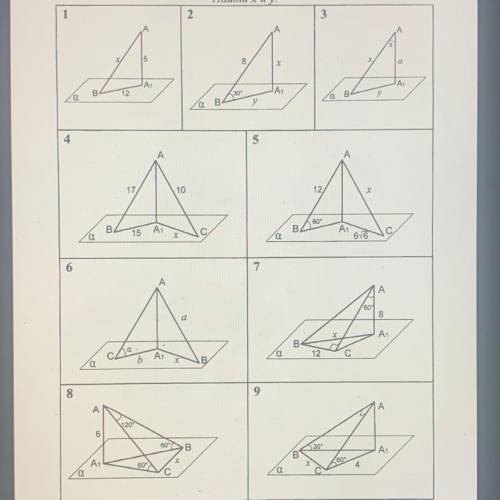
Стереометрия. 10 класс. Таблица 10.11. Перпендикуляр и наклонная.
АА, — перпендикуляр к плоскости a, AB и AC – наклонные.
Найти x и y.

Для начала, давайте разберемся с терминами, которые используются в данном вопросе.
Перпендикуляр - это линия или отрезок, который образует прямой угол (90 градусов) с другой линией или плоскостью.
Наклонная - это линия или отрезок, который не образует прямого угла с другой линией или плоскостью.

Дано:
AA - перпендикуляр к плоскости a,
AB и AC - наклонные.

Теперь перейдем к заданию. Нам нужно найти значения x и y.

Для начала, давайте обратимся к таблице 10.11, которая поможет нам сформировать правила для решения этой задачи.
В таблице нам дают следующие правила:

1) Перпендикуляр к плоскости задается двумя наклонными пересекающимися отрезками.

2) Если на одной наклонной даны две точки A и B, а на другой наклонной точка C, причем AC = BC, то A и B - симметричны относительно плоскости.

Теперь вернемся к изображению. Мы видим, что в плоскости a есть две наклонные линии AB и AC, и перпендикуляр AA пересекает их.
Запишем известные значения:

AB = 3x - 2y
AC = 2x + y

Согласно правилу 2, мы можем заметить, что точки B и C должны быть симметричными относительно плоскости a, так как AC = BC.
Поэтому можно записать равенство:

2x + y = 3x - 2y

Теперь перенесем все члены с "x" на одну сторону и все члены с "y" на другую сторону уравнения:

2y + 2x = 3x - y

Далее, сложим y с обеих сторон, чтобы избавиться от переменной "y":

3y + 2x = 3x

Теперь отнимем 2x от обеих сторон:

3y = 3x - 2x

3y = x

Как мы видим, получили, что 3y = x. Это значит, что x равно 3 раза больше y.

Таким образом, ответ на вопрос "Найти x и y" будет:
x = 3y