1. Геометрия
  2. Составь уравнение окружности с

Составь уравнение окружности с диаметром АВ, если: a) A(-3; 6), B(1; -4);
б) A(-1; 5), B(4; 3).

скмниниручвк скмниниручвк    3   25.08.2022 15:05    3

Ответы
canay2211canay canay2211canay  25.08.2022 15:06

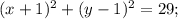
а) {(x + 1)^2} + {(y - 1)^2} = 29;

б) {\left( {x - \frac{3}{2}} \right)^2} + {(y - 4)^2} = \frac{{29}}{4}

Объяснение:

Если точки A({x_1};\,\,{y_1}) и B({x_2};\,\,{y_2}) являются концами отрезка, то его серединой будет точка

O\left( {\displaystyle\frac{{{x_1} + {x_2}}}{2};\,\,\displaystyle\frac{{{y_1} + {y_2}}}{2}} \right).

Эта точка и будет являться центром окружности, а расстояние до любого из концов отрезка — радиусом.

Расстояние между точками A({x_1};\,\,{y_1}) и B({x_2};\,\,{y_2}) находим по формуле

d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} .

Зная центр окружности O({x_0};\,\,{y_0}) и ее радиус R, записываем уравнение

{(x - {x_0})^2} + {(y - {y_0})^2} = {R^2}.

а)

O\left( {\displaystyle\frac{{ - 3 + 1}}{2};\,\,\displaystyle\frac{{6 - 4}}{2}} \right);O( - 1;\,\,1);R = AO = \sqrt {{{( - 1 - ( - 3))}^2} + {{(1 - 6)}^2}} = \sqrt {4 + 25} = \sqrt {29} ;{(x + 1)^2} + {(y - 1)^2} = 29.

б)

O\left( {\displaystyle\frac{{ - 1 + 4}}{2};\,\,\displaystyle\frac{{5 + 3}}{2}} \right);O\left( {\displaystyle\frac{3}{2};\,\,4} \right);R = AO = \sqrt {{{\left( {\displaystyle\frac{3}{2} - ( - 1)} \right)}^2} + {{(4 - 5)}^2}} = \displaystyle\frac{{\sqrt {29} }}{2};{\left( {x - \displaystyle\frac{3}{2}} \right)^2} + {(y - 4)^2} = \displaystyle\frac{{29}}{4}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
hoylli333 hoylli333  19.10.2020 06:27
От стороны развернутого угла АОС в одну полуплоскость отложены СОК=50°и найдите угол между бессиктрисами углов ДОК и АОД​ БЫСТРЕЕЕ СОР...
Andylov Andylov  19.10.2020 06:27
какие из свойств квадрата являются свойствами прямоугольника, какие - ромба, а какие - параллелограмма?...
умка222 умка222  06.12.2019 18:44
Вычисли dbe, если dbc = 40 градусов....
sasharudich sasharudich  06.12.2019 18:41
Втетраэдре dabc все ребра равны a.точки а1.в1 и с1-серредины ребер da,db и dc соответственно а)постройте сечение тетраэдра ,проходящее через точку с1 б)найдите площадь...
vladilichev vladilichev  18.10.2020 22:19
В треугольнике ABC проведена медиана AM. Периметр треугольника ABС равен 80, периметр треугольника AВM равен 76, периметр треугольника AМС равен 68. Найдите медиану...
akotkina1 akotkina1  18.10.2020 22:20
На прямой AB найти точку C, отстоящую от горизонтально-проецирующей плоскости альфа на расстоянии 40ммА(90,25,50)В(50,10,25)Альфа(х)=40ммАльфа(у)=40мм...
89836331552 89836331552  18.10.2020 22:21
с Геомерией 9 класс Найди вектор суммы данных векторов по закону многоугольника (подумай, как применить этот закoн без рисунка; нулевой вектор обозначай через 0). a....
cobaka2705 cobaka2705  28.05.2019 07:50
Одна из сторон прямоугольника равна 91 см,а его диагональ 109 см.найдите вторую сторону прямоугольника. можно с рисунок...
Алина1116577 Алина1116577  28.05.2019 07:50
Вершины четырехугольника abcd расположены на окружности.докажите что сумма двух противоположных углов этого четырёх угольника равна 180 градусов...
Luiza211 Luiza211  28.05.2019 07:50
Вd – биссектриса равнобедренного треугольника авс с основанием ас. периметр ∆авс = 50 см, периметр ∆авd = 30 см. найдите bd....

Популярные вопросы