Содного конца хорды проведена касательная,а а расстояние с другого конца до этой касательной 6 см. длина хорды 10 см. найдите радиус окружности.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1 вопрос. Решите задачу. На экране отображён рисунок из n цветов размеров,...
3 - 30. 3. Нитраты это а) соли фосфорной кислоты; 6) вещества, плохо растворимые...
2 - Заполните таблицу по тексту Муму И.С.Тургенева...
1 - . Мнанын жауабын тауып береныздершы плз...
3 - Твір на тему зустріч з моїми одноклассниками через 15-20 років....
2 - Найди в градусах величину центрального угла на рисунке между точками...
3 - 5-тапсырма. Мәтіндегі негізгі ойды бес сөйлеммен жазыңдар. Түсіндірмелі салалас...
1 - Интернет – неотъемлемая часть жизни молодежи Прочитай текст. Определи основную...
1 - Комектесісіндерші өтінемін...
3 - Дая 10 предложений о том что такое героизм в наше веремя?...
2
Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=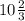 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=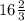 см⇒
см⇒