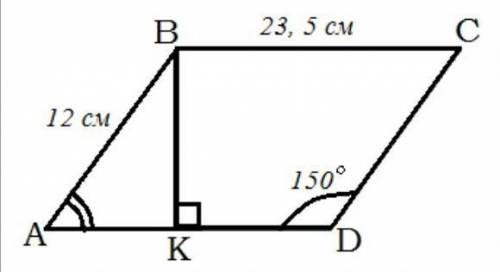
Смежные стороны параллелограмма равны 23,5 см и 12 см, а его тупой угол равен 150°. Найдите площадь параллелограмма (дано/найти/решение).​

Для нахождения площади параллелограмма, нам понадобятся данные о его сторонах и углах. У нас уже имеется информация о смежных сторонах параллелограмма - 23,5 см и 12 см, а также о тупом угле - 150°.

Для решения задачи, мы можем использовать формулу для вычисления площади параллелограмма:

S = a * h

где S - площадь параллелограмма, а - длина одной из его сторон, h - высота, опущенная на эту сторону.

Нам известны две смежные стороны параллелограмма - 23,5 см и 12 см, но нам необходимо найти значение высоты, чтобы воспользоваться формулой.

Для этого нам понадобятся знания о геометрических свойствах параллелограмма.

Параллелограмм имеет две пары равных противоположностоящих сторон и два параллельных противоположностоящих угла.

Также известно, что сторона параллелограмма, на которую опускается высота, является основанием.

У нас есть тупой угол параллелограмма, который составляет 150°. Так как противоположные углы параллелограмма равны, другой угол также будет тупым, то есть равным 150°.

Таким образом, проведя высоту на основание, мы разобьем параллелограмм на два треугольника. Для каждого треугольника будем знать значение одной его неравной стороны и величину двух углов.

Мы можем воспользоваться формулой для нахождения площади треугольника:

S_treug = (1/2) * a * b * sin(γ)

где S_treug - площадь треугольника, a и b - длины сторон треугольника, γ - угол между этими сторонами.

В нашем случае мы имеем треугольник с двумя сторонами - 23,5 см и 12 см, и углом γ, равным 150°.

Для нахождения площади каждого треугольника, мы будем использовать формулу:

S_treug = (1/2) * a * b * sin(γ)

Для первого треугольника мы будем использовать сторону 23,5 см и угол 150°:

S_treug1 = (1/2) * 23,5 см * 12 см * sin(150°)

А для второго треугольника мы будем использовать сторону 12 см и угол 150°:

S_treug2 = (1/2) * 12 см * 23,5 см * sin(150°)

После того, как мы найдем значения площадей обоих треугольников, мы можем сложить их, чтобы получить общую площадь параллелограмма:

S = S_treug1 + S_treug2

Таким образом, мы можем рассчитать площадь параллелограмма, используя формулу для площади треугольника и значения известных сторон и углов.