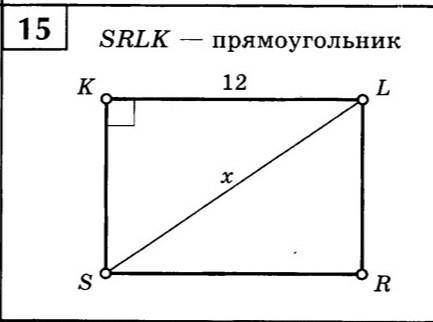
Sl=x
Угол K=90°
Kl=12
Найти : x

Для решения данной задачи, нам необходимо использовать теорему Пифагора, которая гласит: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов".

В данной задаче у нас есть треугольник около буквы L. Дано, что Kl=12 — это один из катетов, а угол K = 90°. Мы должны найти значение стороны Sl=x, которая является гипотенузой.

Для начала, мы можем использовать теорему Пифагора, чтобы выразить значение гипотенузы Sl через два катета:

Sl^2 = Kl^2 + Ll^2,

где Ll - второй катет.

В нашем случае Sl=x, так что получается:

x^2 = Kl^2 + Ll^2.

У нас есть значение Kl = 12. Мы должны найти значение Ll, чтобы решить данную задачу.

Обратимся к прямоугольному треугольнику около буквы K. В нем дано, что угол K=90° и Kl=12. Зная эти значения, мы можем найти значение гипотенузы Lg и катета Kg, используя теорему Пифагора:

Lg^2 = Kl^2 + Kg^2 .

Поскольку у нас есть значение Kl=12, получаем:

Lg^2 = 12^2 + Kg^2 .

Теперь вернемся к прямоугольному треугольнику около буквы L. В нем дано, что угол K = 90° и Kl = 12. Мы знаем, что гипотенуза Lg этого треугольника - это один из катетов треугольника около буквы L, так что получается:

Lg = Ll.

Подставив вместо Lg значение Ll, которое мы хотим найти, получим:

Ll^2 = 12^2 + Kg^2 .

Теперь нам нужно найти значение Kg. Обратимся к нижнему треугольнику около буквы K. В нем дано, что угол K = 90° и Kl = 12. Мы также знаем, что Kl = Ll, так что получается:

Kl = Ll = 12.

Теперь у нас есть значение Kl = 12, так что можем записать уравнение:

12^2 = 12^2 + Kg^2 .

Упростим его:

144 = 144 + Kg^2 .

Вычитаем 144 с обоих сторон уравнения:

0 = Kg^2 .

Это означает, что Kg^2 = 0. Чтобы найти значение Kg, возьмем квадратный корень из обоих сторон уравнения:

Kg = √0 = 0.

Теперь мы можем вернуться к уравнению для Ll:

Ll^2 = 12^2 + Kg^2 .

Подставляем значение Kg = 0:

Ll^2 = 12^2 + 0^2 ,

Ll^2 = 144 + 0 ,

Ll^2 = 144.

Чтобы найти значение Ll, возьмем квадратный корень из обоих сторон уравнения:

Ll = √144,

Ll = 12.

Теперь у нас есть значение Ll = 12. Мы можем использовать его для решения уравнения для x:

x^2 = Kl^2 + Ll^2,

x^2 = 12^2 + 12^2,

x^2 = 144 + 144,

x^2 = 288.

Теперь возьмем квадратный корень из обоих сторон уравнения:

x = √288,

x ≈ 16.97.

Таким образом, ответ на данный вопрос составляет примерно x ≈ 16.97.