1. Геометрия
  2. Скласти рівняння сторін трикутника

Скласти рівняння сторін трикутника заданого своїми вершинами А(2;6) В(4;7)
С

Thevalk3 Thevalk3    3   16.10.2020 06:27    0

Ответы
27sergey1 27sergey1  15.11.2020 06:29

Составим уравнения прямых, проходящих через точки А и В, В и С, А и С - это и будут искомые уравнения.

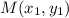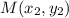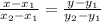Уравнение прямой на плоскости, проходящей через две заданные точки M(x_1,y_1) и M(x_2, y_2), имеет вид \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}.

Для вершин А и В: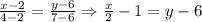 \frac{x-2}{4-2}=\frac{y-6}{7-6}\Rightarrow \frac{x}{2}-1= y - 6. Прямая 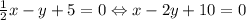\frac{1}{2} x-y+5=0\Leftrightarrow x-2y+10=0 - уравнение стороны АВ.

Для вершин В и С: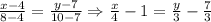 \frac{x-4}{8-4}=\frac{y-7}{10-7}\Rightarrow \frac{x}{4}-1=\frac{y}{3}-\frac{7}{3}. Прямая \frac{1}{4}x-\frac{1}{3}y+\frac{4}{3}=0\Leftrightarrow 3x-4y+16=0 - уравнение стороны ВС.

Для вершин А и С: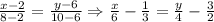 \frac{x-2}{8-2}=\frac{y-6}{10-6}\Rightarrow \frac{x}{6}-\frac{1}{3}=\frac{y}{4}-\frac{3}{2}. Прямая 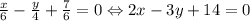\frac{x}{6}-\frac{y}{4}+\frac{7}{6}=0\Leftrightarrow 2x-3y+14=0 - уравнение стороны AC.

ОТВЕТ: AB: x - 2y + 10 = 0; BC: 3x - 4y + 16 = 0; AC: 2x - 3y + 14 = 0.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
королькова1 королькова1  24.06.2019 14:50
Окружность проходит через вершину а прямоугольника abcd и касается сторон bc и cd в точках м и nсоответственно. известно, что вм=24, dn=7. найти площадь прямоугольника abcd.нужно...
JackKalibr JackKalibr  24.06.2019 14:50
Две стороны треугольнка равны 8 и 6 корней из 3, а угол между ними равен 60 градусов. найдите его площадь....
dnaknaf dnaknaf  24.06.2019 14:50
Найти площадь квадрата сторона которого равна 16 см,5,5 см,√a см...
MarinaSc1 MarinaSc1  15.09.2019 05:00
Основою піраміди є прямокутний трикутник із гострим кутом l і катетом a,прилеглим до нього. кожна бічна грань нахилена до основи піраміди під кутом b. знайдіть площу бічної поверхні...
danilkazaytsev danilkazaytsev  15.09.2019 05:00
Обчисліть площу бічної поверхні прямої призми, в основі якої лежить ромб із діагоналями 2 і 2√3 см, а більша діагональ призми утворює з площиною основи кут 60°....
2458k 2458k  15.09.2019 05:00
Найти площадь равнобедренной трапеции у которой высота 7 см и делит основание на два отрезка, наибольшая из которых равна 9 см...
sait14 sait14  15.09.2019 05:00
Дан параллелограм авсd ав=20см; ad=48см; угол а=45 градусам найти площадь параллелограма 8 класс...
Анна111111115 Анна111111115  12.01.2021 07:37
Дано: треугольник АВС уголВ =108° ВС=5 уголА =30° .Найти АВ.​...
pedyxa12 pedyxa12  12.01.2021 07:38
Найдите площадь фигуры, показанной на рисунке...
Lisakwon Lisakwon  12.01.2021 07:40
Самостоятельное решение задач в тетради ФО – По чертежу и записям под ним, запишите в тетради верные равенства или исправьте, чтобы оно было верно Записать ВЕРНО утвержденияа)Угол...

Популярные вопросы