1. Геометрия
  2. Шар радиусом 3см имеет в середине

Шар радиусом 3см имеет в середине пустоту радиусом 2см. чему равен объем шарового слоя? ответ должен получиться примерно такой ≈25,3писм³.

aaaaa123456789p aaaaa123456789p    3   03.03.2019 17:40    2

Ответы
Apple008 Apple008  24.05.2020 00:23

Объём шара: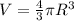 V=\frac{4}{3}\pi R^3

Объём большого шара, у него R = 3 см

V=\frac{4}{3}*\pi*3^3=3^2*4*\pi=9*4*\pi=36\pi см³.

Объём маленького шара, у него R = 2 см

V=\frac{4}{3}*\pi*2^3=\frac{8*4}{3}\pi=\frac{32\pi}{3} см³

Объём шарового слоя это объём большого шара - объём малого:

36\pi-\frac{32\pi}{3}=\frac{108\pi-32\pi}{3}=\frac{76\pi}{3}\approx25,3\pi см³

ответ: 25,3 см³

ПОКАЗАТЬ ОТВЕТЫ
cifirka5 cifirka5  24.05.2020 00:23

Объём всего шара, без пустоты внутри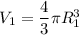  V_1 = \dfrac 43\pi R_1^3

Пустота внутри шара - это тоже шар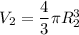   V_2 = \dfrac 43\pi R_2^3

Тогда объём шара, внутри которого пустота

V=V_1-V_2=\dfrac 43\pi R_1^3 - \dfrac 43\pi R_2^3=\\\\\\=\dfrac 43\pi \Big(R_1^3-R_2^3\Big)=\dfrac 43\pi \Big(3^3-2^3\Big)=\dfrac 43\pi \cdot 19

\boxed {\boldsymbol {V=\dfrac{76\pi }3 \approx 25,3\pi~cm^3}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Иришка2007Шеховцова Иришка2007Шеховцова  23.02.2021 23:39
решить с 1.20 по 1.24, На плоскости даны окружность и точка A. Найти множество середин отрезков AN, где N - произвольная точка данной окружности....
Frasmus Frasmus  23.02.2021 23:39
Катет прямокутного трикутника відносится до гіпотенузи цього трикутника , як 2 : 7 . Знайдіть гострі кути цього трикутника...
Topergggg Topergggg  23.02.2021 23:33
Треугольник МРК- равнобедренный, МК - основание. Докажите, что треугольники AMD и BKC равны, если АМ = ВК, МС = DК. (А принадлежит МР, т.В- РК...
Alina12345611109 Alina12345611109  23.02.2021 23:32
2. Используя теорему о внешнем угле треугольника, найдите угол A.​ ОЧЕНЬ...
2001maks44 2001maks44  23.02.2021 23:31
Дан аараллелограмм, у которого АВ=15, ВД=8, АД=16. Найти площадь параллелограмма...
Aaa1nuchto Aaa1nuchto  20.01.2020 20:29
Отрезок ad является бессиктрисой триугольника abc найдите bd и dc если ab=14bc=20ac=21​...
maxim9510 maxim9510  20.01.2020 20:30
Ть розв язати вправи треба якнайшвидше....
gasisivlasova gasisivlasova  20.01.2020 20:30
7класс , решить 2 (на картинке ) 40...
sakulich05 sakulich05  20.01.2020 20:33
Как можно доказать что площадь трапеции равна двух площадей треугольника на площадь прямлугольника....
Франц11 Франц11  20.01.2020 19:07
Точки mi k належать відповідно бічним сторонамab і bc рівнобедреного трикутника abc, am = ск.відрізки ак і см перетинаються в точці о. доведіть,що трикутник aoc...

Популярные вопросы