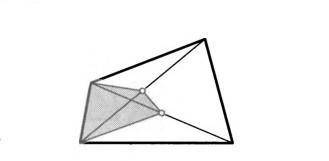
Середины диагоналей выпуклого четырехугольника соеди­ нили с двумя его вершинами так, как это показано на рисунке. Ка­
кую часть от площади четырехугольника составляет закрашенная
фигура?​

Чтобы решить эту задачу, нам нужно найти площади двух треугольников, сформированных внутри четырехугольника, и затем вычислить отношение площади закрашенной фигуры к площади всего четырехугольника.

Шаг 1: Разделим четырехугольник на два треугольника, соединив середины диагоналей с двумя вершинами. Поделим оба треугольника вертикальной линией, как показано на рисунке ниже:

A
/ \
/ \
/______\
D E
/ \ / \
/ \ / \
/_____\___/_____\
B C

Таким образом, получаем два треугольника: ABD и AEC.

Шаг 2: Найдем площадь каждого треугольника, используя формулу для площади треугольника:

Площадь треугольника ABD (S₁) = (база * высота) / 2
Площадь треугольника AEC (S₂) = (база * высота) / 2

Для треугольника ABD:
- База = AC (так как AC является диагональю четырехугольника)
- Высота = AP (так как AP является высотой треугольника ABD)

Для треугольника AEC:
- База = BD (так как BD является диагональю четырехугольника)
- Высота = AQ (так как AQ является высотой треугольника AEC)

Шаг 3: Найдем значения базы и высоты для каждого треугольника.

- База AC можно найти как половину стороны AC (так как AC - это диагональ равнобедренного треугольника ABC, и она делит основание на две равные части).

База AC = 1/2 * AC

- Высота AP мы не знаем, но заметим, что треугольники ABD и ABC подобны (по две стороны в пропорции 1:2). Следовательно, высота треугольника ABD, h, должна быть равна 1/2 высоты треугольника ABC.

Высота AP = 1/2 * h

- База BD можно найти аналогичным образом, делением BD пополам.

База BD = 1/2 * BD

- Высота AQ мы не знаем, но можно заметить, что треугольники AEC и ADC подобны (по две стороны в пропорции 1:2). Следовательно, высота треугольника AEC, k, должна быть равна 1/2 высоты треугольника ADC.

Высота AQ = 1/2 * k

Шаг 4: Выразим базу и высоту через заданные стороны четырехугольника.

- База AC = AD (по условию)
- База BD = BC (по условию)
- Высота AP = 1/2 h (по построению)
- Высота AQ = 1/2 k (по построению)

Шаг 5: Выразим площади каждого треугольника через известные значения.

- Площадь треугольника ABD (S₁) = (AD * 1/2 h) / 2
- Площадь треугольника AEC (S₂) = (BC * 1/2 k) / 2

Шаг 6: Вычислим площади треугольников.

В данной задаче мы не знаем длины сторон и высоты, поэтому без дополнительной информации невозможно вычислить конкретное значение площадей треугольников и, соответственно, часть площади закрашенной фигуры от площади четырехугольника.

Таким образом, мы не можем дать конкретный ответ на данный вопрос без недостающей информации.