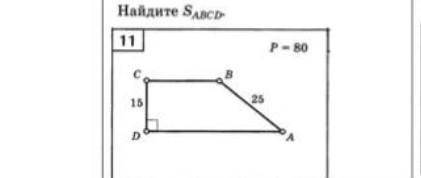
Сделайте задание.Найдите площадь трареции​

Хорошо, давайте разберемся с этим заданием.

У нас дана фигура, которую называют трапецией. Трапеция имеет две параллельные стороны: одна из них называется основанием большая основа (в данном случае AB), а другая - меньшая основа (в данном случае CD). Еще у трапеции есть две наклонные стороны (AD и BC), которые не являются параллельными и соединяют соответствующие вершины оснований.

Для нахождения площади трапеции нам нужно знать длины ее оснований (AB и CD) и высоту (длину перпендикуляра, опущенного из одной вершины трапеции на противоположное основание).

Итак, давайте сначала найдем высоту трапеции. Посмотрите на изображение и найдите точку E, где прямая CE пересекает прямую AB в прямом углу. Заметим, что прямые CE и AD являются высотами трапеции.

Теперь мы можем оценить длину высоты (CE). Обратите внимание на треугольник ACE, он равнобедренный, потому что его две боковые стороны (AC и CE) равны. Таким образом, у нас есть две равные стороны и два равных угла, следовательно, у нас есть равные треугольники.

Зная, что сторона EA (равная CE в данном равнобедренном треугольнике) равна 4 см, мы можем найти длину высоты.

После того, как мы нашли высоту (CE), можно найти площадь трапеции, умножив сумму ее оснований (AB и CD) на высоту. В нашем случае основание AB равно 12 см, а основание CD равно 6 см.

Итак, площадь треугольника вычисляется по формуле: S = (a + b) * h / 2.

S = (AB + CD) * CE / 2
S = (12 + 6) * 4 / 2
S = 18 * 4 / 2
S = 72 / 2
S = 36

Таким образом, площадь данной трапеции составляет 36 квадратных сантиметров.