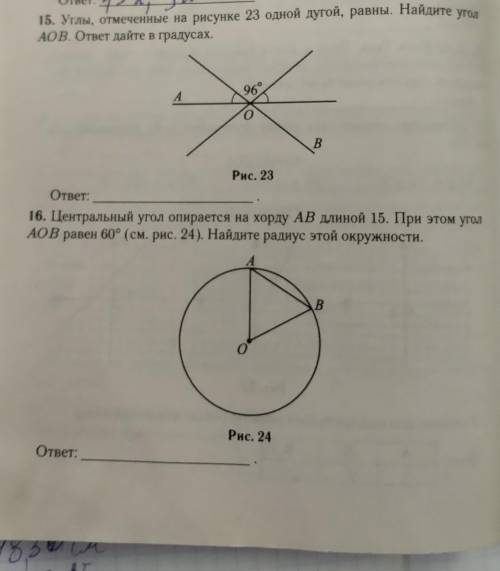
сделать 15 и 16 задание с решением
Другие вопросы по теме Геометрия
Популярные вопросы
- Приведи примеры групп и пластической деформации...
1 - 1. Шешендік сөздердің алғашқы үлгілерін кездестіруге болатын нұсқа...
1 - Зачитайте портрет Максима Яценка. Сліпий музикант ...
2 - и 13 задание хотя бы одно >...
1 - Обчисліть об єм етену, який можна одержати, використавши 1,8 моль...
1 - Көліктің қандай кемшілігі бпр тез жауап күтем...
3 - Як називала австрійська влада Українців?...
3 - Можно сделать все задания ...
2 - як ви розумієте цитату У мене немає ноги й руки,та є очі.У малого...
3 - На какие группы делят боковые почки? ...
2
15. 138°; 16. 15;
Объяснение:
15.
Пусть х - градусная мера угла, обозначенного одной дугой, тогда развёрнутый угол, равный 180°, состоит из угла, равного 96°. и двух углов по х°.
Найдём угол х:
180° = 96° + 2х
2х = 84°
х = 42²
Угол АОВ равен вертикальному углу, состоящему из угла 96° и угла х = 42°, поэтому
∠АОВ = 96° + 42° = 138°.
16.
На рисунке ОА = ОВ = R - радиус окружности.
Следовательно, Δ АОВ - равнобедренный и
∠А = ∠В = 0,5 · (180° - ∠АОВ) = 0,5 · (180° - 60°) = 60°.
Все внутренние углы треугольника АОВ равны между собой, следовательно, ΔАОВ - равносторонний, и радиус окружности
ОА = ОВ = AB = R = 15.
Объяснение:
15. отмеченный угол - (180-96)/2=42°;
∡АОВ=96+42=138° (сумма двух вертикальных углов).
16. ΔАОВ равнобедренный (АО, ВО радиусы) ⇒ ∡А=∡В=(180-60)/2=60° ⇒ ΔАОВ равносторонний ⇒АО=АВ=15 ед.