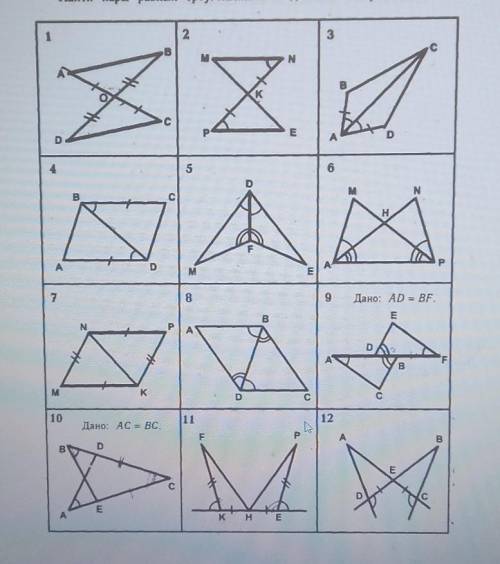
Самостоятельная работа. Первый признак равенства треугольников. Выбрать задания, в которых применяется первый признак равенства треугольников. Выписать дано, найти, и записать третий элемент(по двум сторонам и углу между ними

Добрый день, дорогой школьник! Сегодня мы будем разбирать первый признак равенства треугольников. Этот признак гласит, что если у двух треугольников все соответствующие стороны и углы равны, то эти треугольники равны.

Для выполнения самостоятельной работы выберем несколько заданий, в которых применяется первый признак равенства треугольников. Начнем с задания 1.

Задание 1:
Дано: AB = PQ, BC = QR, ∠ABC = ∠PQR
Найти: AC = ? ∠ACB = ? ∠PQR = ?

Для решения этой задачи нам нужно сравнить соответствующие стороны и углы треугольников ABC и PQR. Мы уже знаем, что AB = PQ, BC = QR и ∠ABC = ∠PQR. Теперь найдем третий элемент. Для этого используем свойства треугольника.

Так как сумма углов треугольника равна 180 градусов, мы можем найти ∠ACB, если знаем, что ∠ABC + ∠ACB + ∠CAB = 180 градусов. В данной задаче у нас уже известно, что ∠ABC = ∠PQR, поэтому можем записать уравнение: ∠PQR + ∠ACB + ∠CAB = 180 градусов.

Также, используя свойства равенства треугольников, можем сказать, что сторона AC равна стороне PR, так как сторона AC соответствует стороне PR.

Таким образом, ответ на задание 1: AC = PR, ∠ACB = ∠PQR, ∠CAB = 180 - (∠PQR + ∠ACB).

Перейдем к заданию 2.

Задание 2:
Дано: DE = FG, ∠EDF = ∠FGH, ∠EFD = ∠FHG
Найти: EF = ? ∠EDF = ? ∠FGH = ?

Для решения этой задачи аналогично заданию 1 мы сравниваем соответствующие стороны и углы треугольников DEF и FGH. Зная, что DE = FG, ∠EDF = ∠FGH и ∠EFD = ∠FHG, мы можем найти третий элемент.

Здесь для нахождения EF, ∠EDF и ∠FGH нам понадобится использовать те же самые свойства и формулы, что и в первом задании.

В результате решения задания 2 мы получим: EF = FG, ∠EDF = ∠FGH, ∠EFD = ∠FHG.

Надеюсь, что объяснение было понятным и ответы на задания были правильно найдены. Если у тебя остались какие-либо вопросы, не стесняйся задавать их!