Самостійна робота з геометрії з подальшою самоперевіркою. Підготовка до КР з теми: "Декартові координати на площині"
1. Визначити радіус і координати центра кола, заданого рівнянням: (х+8)
2
+у2
= 25.

2. Знайти кутовий коефіцієнт прямої: 2х – у - 10 = 0.
3. Установити відповідність між рівняннями кіл і прямих (1-4) та точками, які їм
належать (А-Д):
1. у = -3х – 8 А (6; 1)
2. (х +1)2

+(у – 2)2 = 10 Б (3;2)
3. у = 0,5х + 2 В (-1; -5)
4. (х – 4)

2 + (у +5)2 = 40 Г (2; 1)
Д ( -4; 0)

4. XY- діаметр кола. Скласти рівняння цього кола, якщо Х (-7; 2) і Y(5; 6).
5. Скласти рівняння прямої, кутовий коефіцієнт якої дорівнює 8 і вона проходить через
точку Р (-1; -9)
6. а) Обчислити значення виразу: cos45° +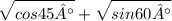
б) Точка А ( 0; 1) належить одиничному колу з центром у початку координат. Який
кут утворює промінь ОА з промінем ОХ, якщо О – початок координат, а ОХ
додатній напрямок осі абсцис? Чому дорівнюють синус і косинус цього кута ?

Student223    2   02.11.2020 13:42    3