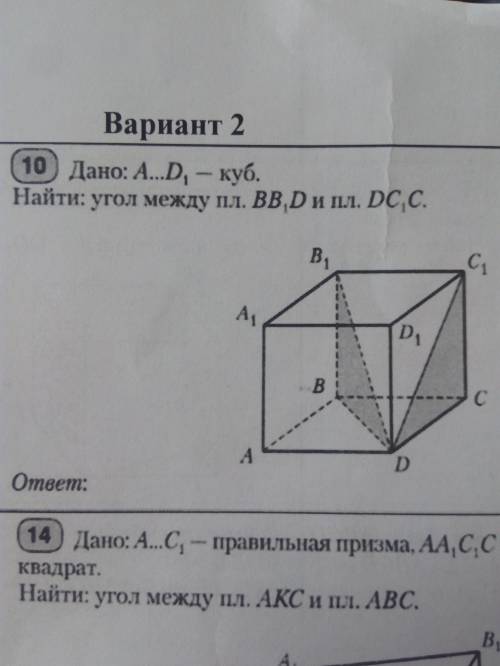
с задачей по геометрии))))) Дано:A...D1-куб. Найти : Угол между пл.BB1D и пл.DC1C
Другие вопросы по теме Геометрия
Популярные вопросы
- Существует ли число произведение цифр которого равно 2004?...
2 - Здійсніть перетворення. дайте назви речовинам. c2h6-c2h2-c6h6-c6h5-no2-c6h5-nh2...
1 - Трём сестрам пять лет назад вместе было 18 лет. сколько лет будет трём...
1 - Представьте выражение 3x-2+5x^2\2x в виде дроби...
3 - Будет сллнце-пойдём гулять.почему тире?...
1 - Надо написать сочинение на тему понравился ли вам фильм один дома 40 слов...
2 - За 5 мілі секунд магнітний потік що пронизує контур змінюється з 9 до...
3 - Сравнить функции симпатической и парасимпатической нервной системы...
3 - Встоловой предлагают 4 разных супа, 5 мясных блюда и 3 десерта. сколько...
2 - Где ставить запятую или точку .и.дя обожаю этот сериал.вы самые лучшие....
2
В данной задаче у нас есть куб с вершинами A, B, B1, C и D1. Также, нам нужно найти угол между плоскостью, образованной точками B, B1 и D, и плоскостью, образованной точками D, C1 и C.
Шаг 1: Нахождение нормалей плоскостей
Чтобы найти угол между плоскостями, сначала необходимо найти их нормали.
Нормалью плоскости является вектор, перпендикулярный этой плоскости. Для нахождения нормали плоскости B, B1, D, мы можем использовать два вектора: BB1 и BD. Вектор BB1 можно найти, вычитая из координаты точки B1 координаты точки B:
BB1 = B1 - B
Аналогично, вектор BD можно найти, вычитая из координаты точки D координаты точки B:
BD = D - B
Шаг 2: Нахождение угла между векторами
У нас есть два вектора: BB1 и BD. Чтобы найти угол между ними, мы можем воспользоваться формулой скалярного произведения:
cos(θ) = (BB1 • BD) / (|BB1| * |BD|)
где θ - искомый угол, BB1 • BD - скалярное произведение векторов BB1 и BD, |BB1| - длина вектора BB1, |BD| - длина вектора BD.
Шаг 3: Расчет скалярного произведения и длин векторов
Теперь нам нужно вычислить скалярное произведение векторов BB1 и BD, а также их длины.
Скалярное произведение BB1 • BD может быть найдено путем умножения соответствующих координат векторов и их сложения:
BB1 • BD = (x1 * x2) + (y1 * y2) + (z1 * z2)
где x1, y1, z1 - координаты вектора BB1, x2, y2, z2 - координаты вектора BD.
Чтобы найти длину вектора BB1, мы можем использовать формулу:
|BB1| = √(x^2 + y^2 + z^2)
где x, y, z - координаты вектора BB1.
Аналогично, длина вектора BD может быть найдена как:
|BD| = √(x^2 + y^2 + z^2)
где x, y, z - координаты вектора BD.
Шаг 4: Подстановка значений и вычисление угла
Допустим, координаты точек B, B1 и D равны:
B = (x1, y1, z1)
B1 = (x2, y2, z2)
D = (x3, y3, z3)
Сначала вычислим векторы BB1 и BD путем вычитания соответствующих координат:
BB1 = (x2 - x1, y2 - y1, z2 - z1)
BD = (x3 - x1, y3 - y1, z3 - z1)
Затем вычисляем скалярное произведение BB1 и BD:
BB1 • BD = (x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) + (z2 - z1) * (z3 - z1)
И, наконец, находим длины векторов BB1 и BD:
|BB1| = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
|BD| = √((x3 - x1)^2 + (y3 - y1)^2 + (z3 - z1)^2)
Подставляем эти значения в формулу для нахождения угла:
cos(θ) = (BB1 • BD) / (|BB1| * |BD|)
и находим значение угла θ. При необходимости, результат можно перевести в градусы умножением на 180 / π.