с рисунком через вершину косинуса проведена плоскость под углом альфа к плоскости основания. эта плоскость пересекает основу косинуса по хорде, которая видна из центра его основания под углом бета. радиус основания косинуса R. найдите площадь сечения

Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.

Объяснение:

Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=.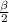

ΔАОК- прямоугольный ,

cos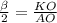 , KO=R*cos;

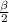sin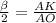 ,AK=R*sin 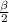,AB=α2Rsin .

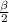ΔSKO прямоугольный ,cos α=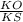, KS=R*cos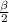/cosα.

S=0,5*AB*SK ,S=0,5*2R*sin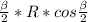/ cosα,

S=0,5*R²*sinβ/cosα=