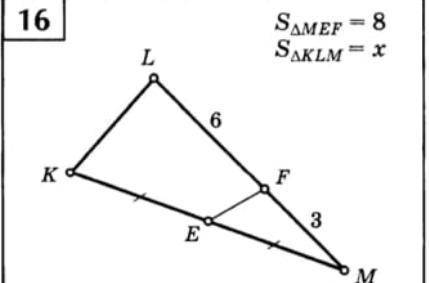
SΔMEF = 8
SΔKLM = x
Необходимо решить задачу с полным решением

Добрый день!

Для решения данной задачи, нам необходимо исследовать треугольники ΔMEF и ΔKLM.

Из задания известно, что площадь треугольника ΔMEF равна 8:
SΔMEF = 8

Мы знаем, что площадь треугольника вычисляется по формуле: S = (1/2) * a * h, где S - площадь, a - основание треугольника, h - высота треугольника.

Для треугольника ΔMEF можно сказать, что основанием является отрезок EF, а высотой является перпендикуляр, опущенный из вершины Δ на основание EF. Давайте обозначим высоту треугольника ΔMEF как hΔMEF.

Теперь давайте посмотрим на треугольник ΔKLM. Из заданного у нас равенства:
SΔKLM = x

Исходя из формулы для площади треугольника, можем сказать, что основанием треугольника ΔKLM является отрезок KL, а высотой является перпендикуляр, опущенный из вершины Δ на основание KL. Обозначим высоту треугольника ΔKLM как hΔKLM.

Теперь, когда мы обозначили высоты каждого треугольника, можем посмотреть на заданное рисунок внимательнее.

Из рисунка мы видим, что треугольники ΔMEF и ΔKLM имеют общую вершину Δ. При этом вершины E и M соединены прямой линией EM, которая перпендикулярна основаниям треугольников EF и KL.

Таким образом, у нас получается два равных треугольника ΔMEF и ΔKLM, потому что у них равны указанные выше высоты hΔMEF и hΔKLM, а сторона ΔM общая для них.

Поскольку треугольники ΔMEF и ΔKLM равны, это означает, что их площади тоже равны. То есть:
SΔMEF = SΔKLM

Известно значение SΔMEF: 8. Подставим это значение в уравнение:
8 = x

Таким образом, мы нашли значение x. Ответ на задачу составляет x = 8.

Надеюсь, данное пояснение помогло вам понять задачу и ее решение. Если у вас все еще остались вопросы, не стесняйтесь задавать их. Я с радостью помогу вам.