С геометрией Задание на фото.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите значение 45 а угол между осью ox и прикосновением, проведенным...
2 - 3. Шлях до підземної печери Зброяра через...До ть будь ласка.А)...
2 - Написать рекламу любого учебника для 6 класса (6-8 предложений)....
1 - Озлобленный, добрый, безобидный, слабый, бесправный, бедный,...
3 - Почему учителя, которые приходят к Журдену, смеются над ним?...
2 - 11.Встановіть відповідність між прізвищами історичних осіб та...
3 - Периметр квадрата дорівнює 2, 8. Чому дорівнюєсторона квадрата?...
3 - Установіть відповідність між героєм повісті о. Гавроша неймовірні...
1 - Задание N 1. Установи соответствие (5 б)1) Титул правителя гунновА)...
3 - Чтобы уверить мальчика в его говорить, Иван Иванович после осмотра...
3
Пусть AC=x, тогда в ΔABC по формуле Герона:
Решим квадратное уравнение относительно x².
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
По формуле связи косинуса и тангенса:
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
По формуле связи косинуса и тангенса:
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=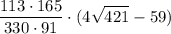 > 113/√421.
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.