с геометрией (нужно решить номера 4 и 5)
С ПОЛНЫМ ответом)

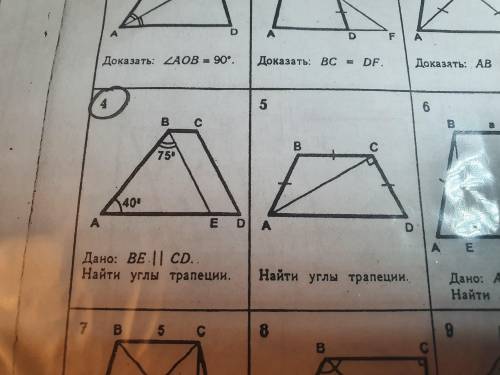
Нахождение углов в трапеции  по готовому чертежу.

Объяснение:

4)ΔАВЕ , по т. о сумме углов треугольника ∠ВЕА=180°-75°-40°=65° .

∠ВЕА=∠СВЕ=65° как накрест лежащие при ВС║АD, ВЕ-секущая , поэтому  ∠АВС=75°+65°=140°.

По т. о внешнем угле для ΔАВЕ , ∠ВЕD=40°+75°=115°

АВСD -параллелограмм и противоположные углы в нем равны⇒ ∠ВСD=115°. Тогда на последний угол ∠D=360°-40°-140°-115°=65°

5) Пусть ∠САD=x, тогда ∠АСВ=х как накрест лежащий при ВС║АD, АС-секущая.

ΔАВС-равнобедренный ⇒∠ВАС=∠АСВ=х ⇒∠ВАD=2х  ⇒∠D=2x т.к трапеция равнобедренная .

ΔАСD-прямоугольный, по свойству острых углов ∠САD+∠D=90° или х+2х=90° , х=30°.

Углы трапеции равны ∠D=∠A=60° , ∠BCD=90°+30°=120° , ∠ABC=120°

4. угол ВАD = 40 градусов

угол АВС = 140 градусов

угол АDC = 65 градусов

угол DCB = 115 градусов

5. угол ВАD = 60 градусов

угол АВС = 120 градусов

угол АDC = 60 градусов

угол ВСD = 120 градусов

Объяснение:

4. рассмотрим треугольник ABE:

сумма углов любого треугольника = 180 градусов.

угол ВАЕ + угол АВЕ + угол ВЕА = 180

угол ВАЕ и угол АВЕ даны.

40 + 75 + угол ВЕА = 180

угол ВЕА = 180 -75 - 40 = 65 градусов.

угол ВЕА и угол ВЕD смежные. сумма смежных углов = 180 градусов.

угол ВЕА + угол ВЕD = 180

угол ВЕD = 180 - 65 = 115 градусов.

рассмотрим параллелограмм ВСЕD. это параллелограмм, так как ВЕ || СD по условию, а ВС || ЕD, так как АВСD - трапеция.

в любом параллелограмме сумма двух прилежащих углов = 180 градусов.

угол ВЕD + угол ЕВС = 180

угол ЕВС = 180 - 115 = 65 градусов

угол ВЕD + угол ЕDC = 180

угол ЕDC = 180 - 115 = 65 градусов

угол ЕDC + угол DCB = 180

угол DCB = 180 - 65 = 115 градусов

рассмотрим угол АВС.

угол АВС = угол АВЕ + угол ЕВС

угол АВС = 75 + 65 = 140 градусов.

угол ВАЕ и угол ВАD - это разные обозначения одного угла;

угол EDC и угол ADC - это разные обозначения одного угла.

ответ: 4 угла трапеции:

угол ВАD = 40 градусов

угол АВС = 140 градусов

угол АDC = 65 градусов

угол DCB = 115 градусов

5. рассмотрим треугольник АВС.

этот треугольник равнобедренный по условию.

в любом равнобедренно треугольнике углы, противолежащие равным сторонам, равны.

угол ВАС = угол ВСА

АВС - треугольник: сумма углов = 180 градусов

угол ВАС + угол ВСА + угол АВС = 180

2 × угол ВАС + угол АВС = 180

рассмотрим трапецию АВСD. она равнобедренная, так как дано, что АВ = СD.

в любой равнобедренной трапеции углы при любом основании равны.

угол АВС = угол ВСD

угол ВСD = угол АСВ + угол АСD

угол АСD = 90 - это дано

угол ВСD = угол АСВ + 90

тогда

угол АВС = угол АСВ + 90

угол АВС = угол ВАС + 90

у нас получилась система уравнений:

2 × угол ВАС + угол АВС = 180

угол АВС = угол ВАС + 90

решим систему: подставим второе уравнение в первое:

2 × угол ВАС + угол ВАС + 90 = 180

3 × угол ВАС = 90

угол ВАС = 30 градусов

подставим в первое уравнение:

2 × 30 + угол АВС = 180

угол АВС = 180 - 60 = 120 градусов

Тогда и угол ВСD = 120 градусов.

в любой равнобедренной трапеции сумма противоположных углов = 180 градусов.

угол ВАD + угол BCD = 180

угол ВАD = 180 - 120 = 60 градусов

угол АВС + угол АDC = 180

угол ADC = 180 - 120 = 60 градусов

ответ: 4 угла трапеции:

угол ВАD = 60 градусов

угол АВС = 120 градусов

угол АDC = 60 градусов

угол ВСD = 120 градусов