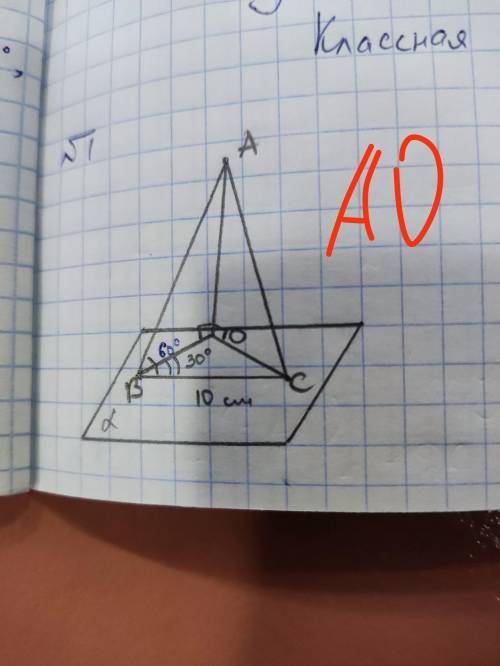
С ГЕОМЕТРИЕЙ. Найти перпендикуляр АО

ответ :       АО = 10√6/3 см .

Объяснение:

   У наведеній умові задачі не вистачає данних .

  Припускаю , що ОВ = ОС . Проведемо висоту ОМ  в ΔВОС , який

   є рівнобедреним .  Висота  ОМ є і медіаною ΔВОС :   ВМ = МС = 5 см .

  ΔВОМ - прямокутний , в якому tg30° = OM/BM ;   OM = BM tg30° =

   = 5 * 1/√3 = 5/√3 ( см ) .

   Внаслідок того , що ΔАОВ = ΔАОС  ,  ΔАВС - рівнобедрений , в

   якого  кут при основі 60° , тому він правильний . Його висота

   АМ = ВС√3/2 = 10√3/2 = 5√3 ( см ) . Так як  АО⊥α , то АО⊥ОМ .

   Із прямок . ΔАОМ :  АО = √ ( АМ² - ОМ² ) = √ ( ( 5√3 )² - ( 5/√3 )² ) =

   = √( 75 - 25/3 ) = √( 8 *75/9 ) = 10√6/3 ( см ) ;         АО = 10√6/3 см .