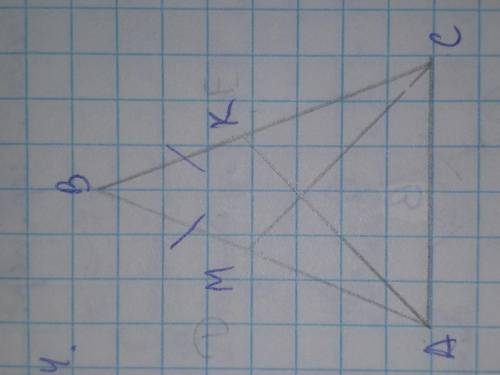
, рисунок уже есть( На бічних сторонах АВ і ВС рівнобедреного трикутника АВС позначили відповідно точки М і К так, що <ВАК =<ВСМ. Доведіть, що ВК = ВМ
Другие вопросы по теме Геометрия
Популярные вопросы
- Упростите вырожение 350•x•2...
1 - Если f(x+1)=3-2x и f(g(x)) =6x-3, найдите g(x) Варианты ответов:А)...
1 - Сократить дроби 122/355 48/100 14/16 4/6 8/24 312/314...
3 - Учебник седьмой класс Юдовская страница 192 по 200 развёрнутый план...
3 - Создерди окы. Екыншы баганга создерди салыстыр. Оларга сурак кой...
3 - На английском Составит туристическую брошюру о городе в Казахстане...
2 - Найдите наименьший целый корень уравнения (1х1-1)(х+2.5)=0...
2 - Каково значение исторического труда А.С.Пушкина История пугачевского...
2 - Выполни деление смешанного числа и обыкновенной дроби (Запиши целое...
2 - Номер 160 система уравнений...
3
У треугольников ABK и MBC угол С - общий, ∠BAK = ∠BCM (по условию) и AB = BC (т.к. ΔABC - равнобедренный), значит ΔABK = ΔMBC по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство соответствующих сторон, т.е. BK = BM. Что и требовалось доказать!