Рисунок для задания 2. 1.Боковая сторона АВ равнобедренной трапеции ABCD равна 18. Найдите длину высоты BM, если AM - 60°
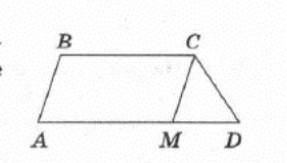
2. На рисунке изображена трапеция ABCD, ее боковые стороны равны 6 и 8, а основания равны 11 и 17.
Найдите периметр треугольника DCM, если
CM ll AB​

Добрый день! Давайте рассмотрим по очереди каждую часть задания.

Задание 1:
Из рисунка видно, что треугольник ABM является равносторонним, так как угол AM равен 60 градусов. Это значит, что все его стороны равны.
Высота треугольника - это отрезок, который перпендикулярен основанию и проходит через вершину. В данном случае, высота треугольника BM перпендикулярна стороне AB и проходит через вершину M.

Если мы разделим треугольник ABM на два прямоугольных треугольника, то получим два прямоугольных треугольника ABC и BCM.

С помощью теоремы Пифагора для прямоугольных треугольников, мы можем найти длину стороны BC в треугольнике ABC и стороны CM в треугольнике BCM.

В треугольнике ABC, где AB - это гипотенуза, а AC и BC - катеты, мы имеем следующее:
AC^2 + BC^2 = AB^2
AC^2 + 18^2 = 6^2
AC^2 + 324 = 36
AC^2 = 36 - 324
AC^2 = -288

Здесь мы получили отрицательное число, что означает, что треугольник ABC не существует. Это означает, что треугольник ABM также не существует и задачу невозможно решить.

Задание 2:
Из рисунка видно, что треугольник DCM создается параллельной линией, проходящей через C и параллельной AB.

Для нахождения периметра треугольника DCM нам нужно найти длины его сторон. Для этого мы можем воспользоваться теоремой Пифагора.

Для начала, нам нужно найти длину стороны DC. Из рисунка видно, что у нас есть прямоугольный треугольник DCL, где DL - это перпендикуляр, опущенный из вершины D на основание AB. Мы знаем, что DL равна 8, так как из условия задачи сторона CD равна 8. Мы также знаем, что LC равна 6, так как это одна из оснований трапеции.

Используя теорему Пифагора, мы можем найти длину стороны DC:
DC^2 = DL^2 + LC^2
DC^2 = 8^2 + 6^2
DC^2 = 64 + 36
DC^2 = 100
DC = √100
DC = 10

Теперь, чтобы найти периметр треугольника DCM, нам нужно найти длины остальных двух сторон - DM и MC.

Если мы посмотрим на треугольник BCM, то увидим, что его стороны BC и MC равны, так как они обе являются боковыми сторонами трапеции. Значит MC = BC = 8.

Также из рисунка видно, что треугольник DCM равнобедренный, так как основания треугольника - это сторона CM и сторона DC, которые равны. Значит, DM = DC = 10.

Периметр треугольника DCM равен сумме длин его сторон:
Периметр = DM + MC + DC
Периметр = 10 + 8 + 10
Периметр = 28

Итак, периметр треугольника DCM равен 28.