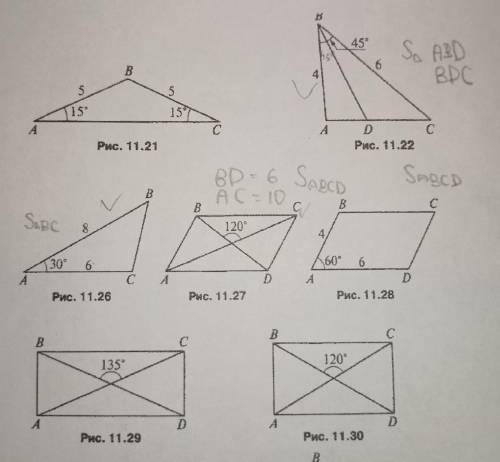
Рис 11.22 найти площадь ABD, BDC, весь угол АВС=45° (BD- биссектриса) рис 11.26 найти площадь АВС
рис 11.27 найти площадь ABCD, если известно, что BD=6, AC=10
рис 11.28 найти площадь ABCD

Находить с синусов

Добрый день! Давайте разберемся с каждым изображением по очереди.

Рисунок 11.22:
Мы видим треугольник ABD, где угол АВС равен 45°, а BD - биссектриса. Чтобы найти площадь треугольника ABD, мы можем использовать формулу площади треугольника: A = (1/2) * основание * высота. В данном случае, основание - это сторона AB, а высота - это расстояние от точки D до стороны AB.

Для начала, нам нужно найти высоту треугольника ABD. Так как BD - биссектриса, она делит угол ABC поровну, то есть угол DBA равен 45/2 = 22.5°.

Теперь, мы можем использовать синус угла DBA, чтобы найти высоту треугольника ABD. Синус угла DBA = противолежащая сторона / гипотенуза, и в нашем случае противолежащей стороной будет высота, а гипотенуза - сторона AB. Мы знаем, что сторона AB равна 10, поэтому нам нужно найти противолежащую сторону.

Высота = синус (22.5°) * 10.

Вычисляем синус 22.5° по таблице или калькулятору и получаем значение 0.3827. Подставляем это значение в формулу:

Высота = 0.3827 * 10 = 3.827.

Теперь у нас есть высота треугольника ABD, чтобы найти площадь, умножим ее на основание:

Площадь ABD = (1/2) * 10 * 3.827 = 19.135 квадратных единиц.

Теперь перейдем к треугольнику BDC.
Мы уже знаем, что BD - биссектриса, поэтому мы можем предположить, что DB и DC равны. Поэтому угол DBC также равен 22.5°.

Также нам известно, что BC = BD = 6.

Для нахождения площади треугольника BDC, воспользуемся той же формулой площади треугольника: A = (1/2) * основание * высота. В данном случае, основание - это сторона BC, а высота - это расстояние от точки D до стороны BC.

Чтобы найти высоту треугольника BDC, мы можем использовать синус угла DBC, как и раньше.

Высота = синус (22.5°) * 6.

Вычисляем синус 22.5° по таблице или калькулятору и получаем значение 0.3827. Подставляем это значение в формулу:

Высота = 0.3827 * 6 = 2.296.

Теперь у нас есть высота треугольника BDC, чтобы найти площадь, умножим ее на основание:

Площадь BDC = (1/2) * 6 * 2.296 = 6.888 квадратных единиц.

Теперь перейдем к рисунку 11.26:
Мы видим треугольник АВС, и нам нужно найти его площадь. Угол АВС здесь равен 45°.
Чтобы найти площадь треугольника АВС, мы снова можем использовать формулу A = (1/2) * основание * высота. В данном случае, основание - это сторона AB, а высота - это расстояние от точки С до стороны AB.

Мы уже знаем, что сторона AB равна 10. Нам остается найти высоту.

Из рисунка видно, что высота состоит из двух отрезков. Для нахождения высоты обратимся к рисунку 11.22. Мы уже нашли одну часть высоты - расстояние от точки D до стороны AB, и оно равно 3.827. Осталось найти вторую часть высоты - отрезок SD.

Обратим внимание, что треугольник ASD прямоугольный, так как его две стороны AS и SD являются радиусами окружности. Поэтому угол ASD равен 90°.

Теперь мы можем использовать соотношение синуса угла ASD для нахождения высоты треугольника СDС.

Синус угла ASD = противолежащая сторона / гипотенуза. В нашем случае, противолежащей стороной будет высота, а гипотенузой - сторона СР. Мы знаем, что СР = 10, поэтому нам нужно найти противолежащую сторону.

Противолежащая сторона = синус (90°) * 10 = 1 * 10 = 10.

Теперь у нас есть вся высота треугольника АВС. Складываем две части высоты: 3.827 + 10 = 13.827.

Подставляем эту высоту в формулу:

Площадь АВС = (1/2) * 10 * 13.827 = 69.135 квадратных единиц.

Перейдем к рисунку 11.27:
Мы видим четырехугольник ABCD, где BD = 6 и AC = 10. Нам нужно найти его площадь.

Чтобы найти площадь четырехугольника ABCD, мы можем разбить его на два треугольника: ABD и BCD. Затем мы найдем площади и сложим их, чтобы получить площадь всего четырехугольника.

Мы уже знаем площадь треугольника ABD: 19.135 квадратных единиц.

Теперь рассмотрим треугольник BCD. У нас есть три стороны BCD: BC = BD = 6, CD = 10 и DB = 6. Мы можем использовать формулу Герона для нахождения площади треугольника, так как у нас известны все стороны.

Формула Герона:
A = √(s * (s - a) * (s - b) * (s - c)),
где s = (a + b + c) / 2 - полупериметр треугольника.

В нашем случае: a = BC = 6, b = CD = 10, c = DB = 6.

Сначала найдем полупериметр:

s = (6 + 10 + 6) / 2 = 22 / 2 = 11.

Теперь подставим значения в формулу Герона:

A = √(11 * (11 - 6) * (11 - 10) * (11 - 6)) = √(11 * 5 * 1 * 5) = √(275) = 16.583 квадратных единиц.

Теперь складываем площади двух треугольников:

Площадь ABCD = 19.135 + 16.583 = 35.718 квадратных единиц.

Перейдем к рисунку 11.28:
Мы видим четырехугольник ABCD, и нам нужно найти его площадь. Нам не даны стороны или углы четырехугольника, поэтому мы не можем использовать ранее описанные методы.

Вместо этого мы можем разбить четырехугольник на два треугольника: ABC и ACD. Затем мы найдем площади и сложим их, чтобы получить площадь всего четырехугольника.

У нас есть два треугольника - ABC и ACD. Чтобы найти их площади, мы можем использовать формулу площади треугольника: A = (1/2) * основание * высота.

Площадь треугольника ABC:
Мы видим, что сторона AC является высотой треугольника ABC. По условию, у нас дано значение AC = 10. Мы также видим прямой угол между сторонами AB и AC, поэтому основание треугольника ABC - это сторона AB.

Площадь ABC = (1/2) * 10 * AB.

Аналогично, площадь треугольника ACD равна (1/2) * 10 * AD.

В данном случае, нам не даны длины сторон AB и AD, поэтому мы не можем найти их площади. Без дополнительной информации мы не можем решить задачу и найти площадь всего четырехугольника.

Мы надеемся, что этот подробный ответ помог вам разобраться с задачей. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!