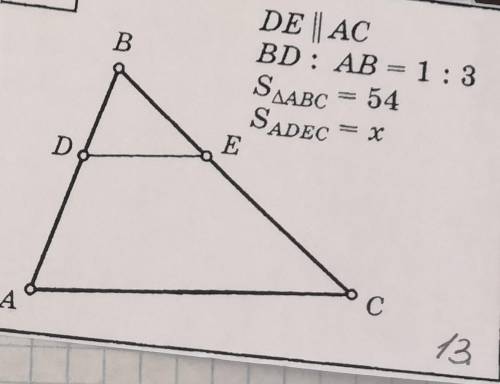
Решите задачу по геометрии условия на фото: DE : AB=1:3
Sтреугол.ABC=54
S ADEC = x
Найти x

Для того чтобы решить эту задачу, нам понадобятся знания о геометрии треугольников и пропорциях.

Пусть S_ABC обозначает площадь треугольника ABC, а S_ADEC обозначает площадь треугольника ADEC. Заметим, что треугольники ABC и ADEC имеют одну общую высоту, так как точка E находится на продолжении стороны AB. Поэтому, отношение площадей этих треугольников будет равно отношению длин их оснований:

S_ADEC : S_ABC = DE : AB (1)

Из условия задачи нам дано, что DE : AB = 1:3. Мы также знаем, что S_ABC = 54 (что значит, что площадь треугольника ABC равна 54).

Заменим в формуле (1) значения DE : AB на 1:3 и S_ABC на 54:

S_ADEC : 54 = 1:3

Теперь мы можем решить эту пропорцию. Для этого умножим оба значения на 54:

S_ADEC = 1/3 * 54

После вычислений мы получим:

S_ADEC = 18

Таким образом, площадь треугольника ADEC равна 18. Ответ: x = 18.