Решите задачу по геометрии.

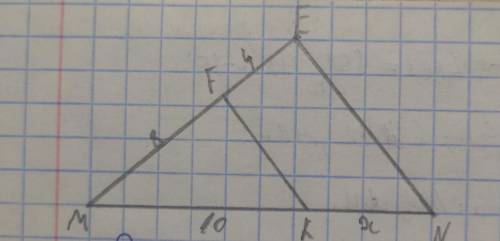
Дано:угол EMK,MF=8;FE=4;MK=10;FK||EM

Найти:KN

Дан угол EMK, в котором известна длина отрезка MF=8, отрезка FE=4 и отрезка MK=10. Также известно, что прямая FK параллельна прямой EM.

Для решения этой задачи по геометрии нам потребуется использовать различные свойства углов и прямых.

Шаг 1: Определение связей между углами и отрезками
В данной задаче нам нужно найти длину отрезка KN. Для этого нам потребуется использовать параллельность прямой FK и прямой EM. По свойству противоположных углов, угол MKF равен углу MKE. Так как MF является продолжением отрезка FE, то угол MFE равен углу MFK. Также, углы MFK и KFE являются вертикальными, поэтому они равны. Таким образом, у нас есть два равных угла - угол MFK и угол KFE.

Шаг 2: Использование свойств равных углов
Из равенства углов MFK и KFE следует, что треугольники MKF и KFE подобны. Поэтому отношение соответствующих сторон этих треугольников равно отношению их высот. То есть отношение длин отрезков MK и KN должно быть равно отношению длин отрезков FE и KE.
MK/KN = MF/KE (1)

Шаг 3: Определение длины отрезка KE
Для определения длины отрезка KE нам понадобится использовать свойство равенства углов KFE и FEM, так как прямая FK параллельна прямой EM. Поэтому треугольники KFE и FEM также являются подобными. Это означает, что отношение длин отрезков KE и EM должно быть равно отношению длин отрезков KF и EF.
KE/EM = KF/EF (2)

Шаг 4: Поиск длины отрезка KE и отрезка KN
Чтобы найти длину отрезка KE, мы можем использовать соотношение, полученное на третьем шаге (уравнение 2). Подставим известные данные в это соотношение:
KE/EM = KF/EF
KE/(FE+EM) = KF/EF
KE/(4+10) = KF/4
KE/14 = KF/4
KE = (KF/4) * 14
KE = (KF * 14) / 4

Теперь, чтобы найти длину отрезка KN, мы можем использовать соотношение, полученное на втором шаге (уравнение 1). Подставим известные данные в это соотношение:
MK/KN = MF/KE
10/KN = 8/((KF * 14) / 4)
10/KN = 8 * 4 / (KF * 14)
10/KN = 32 / (KF * 14)
KN = (KF * 14 * 10) / 32
KN = (KF * 35) / 8

Таким образом, мы получаем ответ: KN = (KF * 35) / 8.

Для более точного решения задачи, нужны значения угла FK или длины отрезка FK. Только с этой информацией можно вычислить длину отрезка KN.