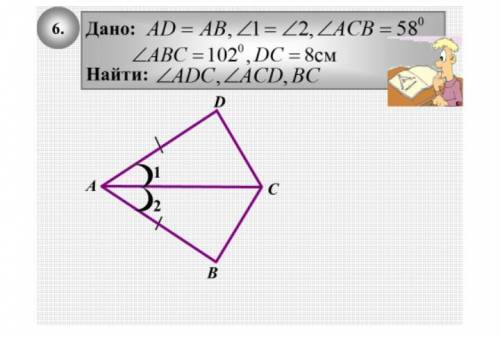
Решите задачу: дано: аd=ab

Угол 1=угол 2

угол acb=58°

угол abc=102°

dc=8 см

найти:

угол аdc,

угол acd,

bc

Дано: ad = ab, угол 1 = угол 2, угол acb = 58°, угол abc = 102°, dc = 8 см.

Нам нужно найти угол аdc, угол acd и bc.

1. Начнем с угла аdc (x). У нас есть два факта, которые связаны с этим углом:

- ad = ab (дано)
- угол 1 = угол 2 (дано)

Используем данные, чтобы решить этот угол.

Так как ad = ab, у нас есть равнобедренный треугольник. Углы при основании равны. Поэтому, угол 1 и угол 2 - это равные углы. Пусть угол 1 = угол 2 = y.

Теперь у нас есть уравнение: y + 58° + 180° - x = 360° (сумма углов треугольника равна 180°, и мы добавляем угол acb и угол abc)
180° + y - x = 360°

Выразим x:
x = 180° + y - 360°
x = y - 180°

2. Теперь найдем угол acd (z).

Мы знаем, что сумма углов треугольника acd равна 180°.
угол acd + угол adc + угол аdc = 180°
z + 102° + x = 180°

Подставим значение x (которое мы нашли ранее):
z + 102° + (y - 180°) = 180°

Выразим z:
z = 180° - 102° - y + 180°
z = -y + 258°

3. Наконец, найдем bc.

Как мы видим на рисунке, треугольник abc - это равнобедренный треугольник, так как ab = ad. Поэтому, углы при основании равны.

Пусть угол acb и угол abc вместе равны k. Тогда, угол bca также равен k.

Теперь мы знаем, что угол bca + угол bac + угол abc = 180°.
k + 58° + 102° = 180°

Сложим углы:
k + 160° = 180°

Выразим k:
k = 180° - 160°
k = 20°

Так как угол bca равен k, мы нашли, что bc = 20°.

Итак, результаты:

Угол аdc (x) = y - 180°
Угол acd (z) = -y + 258°
bc = 20°