Решите задачи . Я не понимаю.
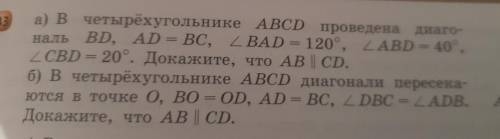
Другие вопросы по теме Геометрия
Популярные вопросы
- Отметь героев сказки Снежная Королева которых можно назвать...
3 - буду очень сильно благодарна...
3 - 2.Соотносит не менее 3 терминов и определений сегодня надо сдать...
3 - Відповідно до рішення Коцюбинської селищної ради Київської області...
1 - 27. 1. Прочитай приклади. Які числівники ти вжив? 60 + 5 = 65...
3 - Тіло здійснює коливання з амплітудою 5 см.яка його максимальна...
2 - Сколько в данном тексте предложений подлежащее в которых выражено...
1 - Где было найден Берельский могильник и сколько круганов в нём...
2 - ответье на аопросы по биологии ток кратенько...
1 - Знайдіть кут в якщо кут а 50...
3
ответ:Номер 1
Треугольник АВD
<ADB=180-(120+40)=20 градусов
<АDB=<CBD=20 градусов,как накрест лежащие при АD || BC и секущей DB
Треугольник АВD равен треугольнику DBC по 1 признаку равенства треугольников-по двум сторонам и углу между ними
АD=BC;<DBC=<ADB;по условию задачи
DB-общая сторона
Равенство доказано,а это значит,что равны и соответствующие стороны и соответствующие углы
<С=<А=120 градусов
<АВD=<BDC=40 градусов ,согласно равенства треугольников,и ещё они являются накрест лежащими углами при АВ || DC и секущей DB
Если при пересечении двух прямых секущей,накрест лежащие углы равны между собой,то прямые параллельны
АВ||DC;AD||BC:
Номер 2
Треугольники АDB и DBC равны между собой по 1 признаку равенства треугольников-по двум сторонам и углу между ними
<DBC=<ADB;AD=BC;DB-общая сторона
Равенство доказано,а значит
АВ=DC;<BDC=<DBA,cогласил равенству треугольников,а также как накрест лежащие при АВ||DC и секущей DB
Если при пересечении двух прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
Объяснение: