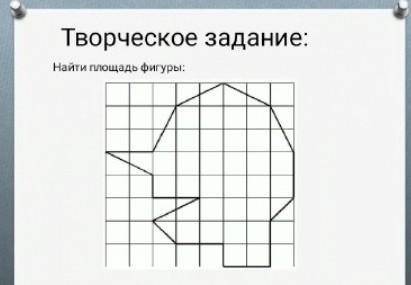
Решите Найдите площадь фигуры.​

Чтобы найти площадь данной фигуры, мы можем разделить ее на две части: прямоугольник и треугольник.

1) Прямоугольник:
На изображении, по которому мы решаем эту задачу, видно, что сторона прямоугольника равна 8 см, а другая сторона - 7 см. Чтобы найти площадь прямоугольника, нужно умножить длину на ширину. Таким образом, площадь прямоугольника будет равна 8 см * 7 см = 56 см².

2) Треугольник:
Чтобы найти площадь треугольника, мы можем использовать формулу площади треугольника:
Площадь треугольника = (основание * высота) / 2.

На изображении видно, что основание треугольника - это сторона прямоугольника длиной 8 см. Для нахождения высоты треугольника, нужно провести перпендикуляр из вершины треугольника до основания.

Так как треугольник является равнобедренным, высота будет проходить через середину основания и перпендикулярно ему, равноотстоять от двух боковых сторон. Поэтому можно условно представить эту высоту как одну из двух одинаковых сторон равнобедренного треугольника.

Таким образом, мы получим два прямоугольных треугольника: один с основанием 8 см, другой с основанием 7 см.

Для подсчета их площади, нам нужно найти высоту каждого из этих треугольников. По теореме Пифагора, для прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае, один катет - это 4 см (половина основания), другой - это недостающая сторона треугольника.

Таким образом, квадрат гипотенузы первого треугольника будет равен: 4² + x² = 8², где x - длина недостающей стороны. Решим это уравнение:
16 + x² = 64
x² = 64 - 16
x² = 48
x = √48
x ≈ 6.93 см (округляем до сотых)

Аналогично, для второго треугольника:
x² + 4² = 7²
x² + 16 = 49
x² = 49 - 16
x² = 33
x = √33
x ≈ 5.74 см (округляем до сотых)

Теперь, когда у нас есть высота каждого треугольника, мы можем найти их площадь. Подставим значения в формулу:
Площадь первого треугольника = (8 см * 6.93 см) / 2 ≈ 27.72 см²
Площадь второго треугольника = (7 см * 5.74 см) / 2 ≈ 20.09 см²

Теперь, чтобы найти общую площадь фигуры, нужно сложить площади прямоугольника и двух треугольников:
Общая площадь фигуры = площадь прямоугольника + площадь первого треугольника + площадь второго треугольника
Общая площадь фигуры ≈ 56 см² + 27.72 см² + 20.09 см²
Общая площадь фигуры ≈ 103.81 см²

Итак, площадь данной фигуры примерно равна 103.81 см².