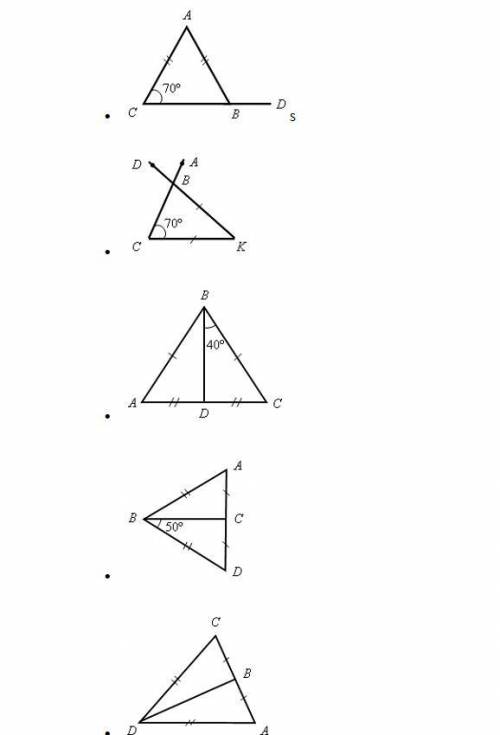
РЕШИТЕ. Найдите DВА. В задачах 3-5 сначала доказать равенство треугольников. (перечертить чертеж, записать условие задачи и решение с пояснениями)

РЕШИТЕ. Найдите DВА. В задачах 3-5 сначала доказать равенство треугольников. (перечертить чертеж, за

Ответы

s1cro 24.01.2024 15:03

Чтобы решить данную задачу, мы должны сначала доказать равенство треугольников. Посмотрим на чертеж задачи.

Задача говорит о нахождении точки DВА. Для начала докажем, что треугольник ABD равен треугольнику ВСD. Для этого нам потребуется несколько шагов.

Шаг 1: Определим соответствующие стороны и углы в треугольниках ABD и ВСD.

В треугольнике ABD у нас есть сторона AB, угол A и сторона BD.
В треугольнике ВСD у нас есть сторона CD, угол C и сторона BD.

Шаг 2: Посмотрим на условие задачи и чертеж. Мы видим, что сторона BD общая для обоих треугольников.

Шаг 3: Для равенства треугольников достаточно доказать, что у них равны две стороны и угол между ними.

Шаг 4: В треугольниках ABD и ВСD мы видим, что сторона AB и сторона CD равны, так как это гипотенузы прямоугольных треугольников и равны по теореме Пифагора.

Шаг 5: Теперь нам нужно доказать равенство угла A и угла C. Мы можем это сделать, используя знание о свойствах геометрических углов.

Шаг 6: По условию задачи мы знаем, что угол BAD равен углу BCD, так как это вертикальные углы и они равны по свойству вертикальных углов.

Шаг 7: Теперь мы видим, что угол ABD и угол CBD - это внутренние углы треугольников, состоящие из угла A и угла C, соответственно. По свойству внутренних углов треугольника, их сумма равна 180 градусам.

Шаг 8: Так как угол ABD и угол CBD равны, и их сумма равна 180 градусам, то угол A и угол C также равны.

Шаг 9: Таким образом, мы доказали, что треугольник ABD равен треугольнику ВСD по двум сторонам и углу между ними.

Теперь, когда мы доказали равенство треугольников, мы можем перейти к нахождению точки DВА.

Шаг 10: Мы видим, что точка DВА - это точка пересечения прямых CD и AB.

Шаг 11: Мы знаем, что точка пересечения прямых может быть найдена как пересечение их уравнений. Уравнение прямой CD можно записать как y = -3x + 6 (мы должны раскрыть скобки и выразить y через x). Уравнение прямой AB можно записать как y = 2x + 4.

Шаг 12: Теперь мы можем приравнять уравнения прямых, чтобы найти координаты точки DВА.

\begin{align*}
-3x + 6 &= 2x + 4\\
-3x - 2x &= 4 - 6\\
-5x &= -2\\
x &= \frac{-2}{-5}\\
x &= \frac{2}{5}
\end{align*}

Шаг 13: Теперь мы можем подставить найденное значение x в одно из уравнений прямых, чтобы найти значение y.

\begin{align*}
y &= 2\left(\frac{2}{5}\right) + 4\\
y &= \frac{4}{5} + 4\\
y &= \frac{24}{5}
\end{align*}

Шаг 14: Таким образом, координаты точки DВА равны (2/5, 24/5).

Итак, мы решили задачу, найдя точку DВА, а также доказали равенство треугольников ABD и ВСD.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия