Решите кому не сложно
очень надо
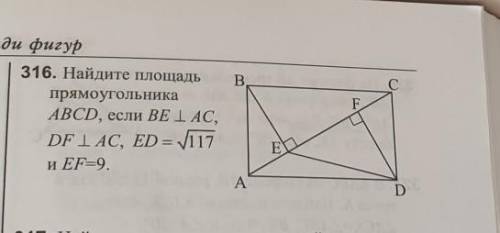
Другие вопросы по теме Геометрия
Популярные вопросы
- Оксид железа (iii) массой 8г обработали раствором соляной кислоты. найдите массу...
3 - Сделайте красворд с ответами по музыке( можно фамилии композиторов) более 15 слов...
3 - Какие внешнеполитические были решены в 16 веке?...
1 - Comparative and superlative adjectives. put the correct form of the adjective into...
3 - Укажите решающий фактор, определивший специализацию эквадора на производстве бананов...
2 - Напишите сочинение окончание 4 класса или похожее минимум 7 предложений...
2 - Втреугольнике авс угол с -прямой, угол а= 58*. на гипотенузу ав из точки f катета...
3 - После семи стирок длина,высота и ширина куска мыла уменьшилась вдвое. на сколько...
1 - Напишите уравнения реакций, с которых можно осуществить превращения: а) ba - bao...
1 - 1. в электронных таблицах выделена группа ячеек а1: в3. сколько ячеек входит в этот...
3
ответ: S = 90
Объяснение:
Сделаем дополнительные построения (на рисунке).
Из треугольника EFD найдем высоту DF.
DF²= ED²-EF² = 117 - 81 = 36 и отсюда DF = 6
В новом параллелограмме BEDF диагонали пересекаются и делятся пополам, значит ОЕ = OF = EF/2 = 4,5
Из треугольника ОFD по Пифагору найдем OD
OD² = OF² + FD² = 4,5²+6² = 56,25 и тогда OD = 7,5
Но диагонали прямоугольника равны и в точке пересечения делятся пополам, то есть АС=BD = 7,2*2 = 15
Теперь найдем синус угла между диагоналями <FOD из того же треугольника OFD
sin(FOD) = ED/OD = 6/7.5 =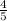
S = 0,5*AC*BD*sin(FOD) = 0,5*15*15*4/5 = 90
ответ:90 ед. кв.
Объяснение:во вложении и более детальнее здесь.
EF=9 DF=√(117-81)=6
По свойству высоты DF, проведенной из вершины D прямоугольного треугольника АВС DF²=АF*FС, АЕ=FC, это следует из равенства прямоугольных треугольников АВЕ и DFC, они равны по гипотенузе (АВ=СD, и острому углу; ∠ВАЕ=∠CDF, это накрест лежащие при АВ║ CD и секущей АС) FC=DF²/EF=36/9=4
Если АЕ=FC=4, то AС=9+8
искомая площадь состоит из двух площадей ΔАВС, т.е. 2*0.5*АС*DF=15*6=90/ед. кв./