Решите геометрическую задачу.

Другие вопросы по теме Геометрия
Популярные вопросы
- Если собака не в силах раскопать пострадавшего, она мчится в селение...
3 - Надо сочинение на тему почему чтение художественной - это труд...
3 - Как социальные сети влияют на речь, язык?...
3 - Эквивалентность логических схем(конспект)...
3 - Какую массу имеет чистая вода,если она занимает объем 1,5 л?...
3 - Диагонали прямоугольника. диагонали прямоугольника авсд пересекаются...
1 - Запишите выражение для нахождения площади квадрата со стороной...
3 - Вкниге 512 страниц. сколько информации содержит сообщение о том,...
1 - Рассмотреть пк как черный ящик, что будет на входе, а что на выходе....
3 - Сколько целых чисел заключено между числами: 10 и корень из 120...
3
//////////////////////////////////////
Snlm=6 кв.см.
Объяснение:
Дано:
ΔABC; Sabc=18 кв.см.
M-точка пересечения его медиан.
AE;BL;CF-медианы.
MK║BC
Найти: Snlm-?
1) LEMC=LNMA - по свойству вертикальных углов.
2) LCNA=LNCB - накрест лежащие углы.
3) ΔCME и ΔAMN - подобные по двум углам (первый признак подобия)
4) По свойствам медианы:
Safm=Sfbm=Sbem=Semc=Smlc=Smal⇒Semc=Sabc/6=18/6=3 кв.см.
5) По свойствам медианы: AM/ME=2/1=2
Так как AM и ME подобные стороны ΔCME и ΔAMN, то коэффициент подобия k=AM/ME=2
6) Зная коэффициент подобия, вычислим Samn:
Samn=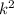 *Scme=
*Scme=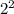 *3=4*3=12 кв.см.
*3=4*3=12 кв.см.
7) Sanc=Sanm+Saml+Slmc=12+3+3=18 кв.см.
8) Медиана-NL делит площадь в ΔANC на две равновеликие части поэтому:
Slnc=Sanc/2=18/2=9 кв.см.
9) Искомая площадь ΔNLM равна:
Snlm=Slnc-Slmc=9-3=6 кв.см.