Решите доказать что если в трапецию можно вписать окружность ,то угол образуемый биссиктрисами углов , прилежащих к боковой стороне, прямой
​

Так основания трапеции параллельны, а углы прилежащих к боковой стороне односторонние углы, то по теореме сумма односторонних углов при параллельны прямых 180 градусов, биссектриса каждого угла делит угол пополам, то есть пусть углы при боковой стороне α и β, тогда α + β = 180 и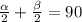 .Пусть биссектрисы пересекаются в точке K, тогда угол K = 180 - (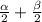)= 180 - 90 = 90, по теореме про сумму углов треугольника.