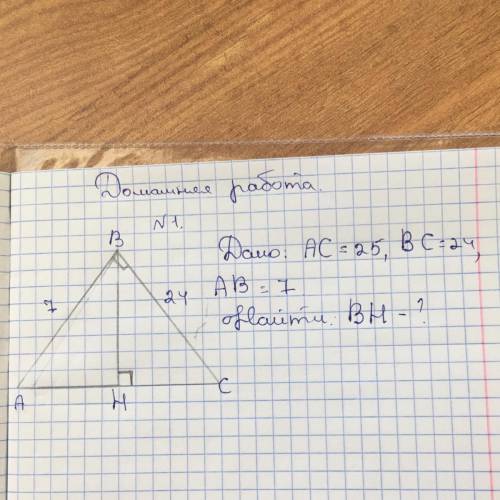
Решите Дано: AC=25, BC=24, AB=7
Найти BH=?

Для решения этой задачи нам понадобятся некоторые знания о геометрии треугольников.

Давайте разберемся, что изображено на данной картинке. Нам дан треугольник ABC, где AC=25, BC=24 и AB=7. Мы хотим найти длину отрезка BH.

Для начала, вспомним основные свойства треугольников. Одно из таких свойств - это теорема Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Похоже, что треугольник ABC является прямоугольным, поскольку одна его сторона является гипотенузой. Давайте проверим это.

Для этого посмотрим на сторону AB. Если квадрат длины стороны AB равен сумме квадратов сторон AC и BC, то треугольник ABC будет прямоугольным. В нашем случае, AB^2=7^2=49, AC^2=25^2=625 и BC^2=24^2=576. Если мы сложим AC^2 и BC^2, получим 625+576=1201, что не равно AB^2. Таким образом, треугольник ABC не является прямоугольным.

Теперь мы можем использовать другой подход для решения этой задачи. Давайте нарисуем перпендикуляр BH, который опущен из вершины B на гипотенузу AC.

Мы знаем, что перпендикуляр опущенный из вершины прямого треугольника на гипотенузу делит его на два подобных треугольника. Также мы знаем, что соотношение сторон подобных треугольников равно.

Таким образом, отношение BH к BC, должно быть таким же, как отношение AB к AC: BH/BC=AB/AC. Подставим значения, которые у нас есть: BH/24=7/25.

Давайте решим это уравнение. Умножим обе стороны на 24: BH=7/25 * 24. Произведение 7/25 и 24 равно 6,72. Значит, BH=6,72.

Таким образом, мы нашли, что длина отрезка BH равна 6,72.